实验-利用CV法测量半导体的杂质分布

摘要： 在半导体工业中，影响元件性能最重要的因素之一是掺杂浓度，因此精准地检测杂质浓度是评估元件好坏的重要环节^[1]。本文章基于单边突变结的耗尽层中无自由电子的假设，模型化的计算了空间电荷区和偏压的定量关系，并将该势垒看作一个间距可变的电容。实验中通过串联标准电容并加交流电压的方法，间接测量P-N结势垒电容。通过改变直流偏置电压，得到杂质掺杂率随着交界距离的变化关系。

关键词：势垒电容，电容电压法，锁相放大，杂质测量，倍频测量

获取实验报告的pdf文件(仅供参考)

引言

1904年，Joseph Thomson在对锗和硅进行性质研究时发现这种材料并不同于一般的导体和绝缘体，这些材料有更加独特的电学性质，他将这种导电性介于导体和绝缘体之间的材料称为半导体^[2]。1947年，John Bardeen，Walter Bratton和William Shockley共同研究发明出了晶体管^[3-4]，开启了现代电子学的时代，使得电子设备体积更小、效率更高。这些研究为21世纪的集成电路和硅基芯片的发展奠定了基础。同时，对于单纯半导体材料的研究并未停止，20世纪70年代，科学家相继提出各种化合物形态的半导体，其中GaAs最有代表性^[5]，其优良的性质使其可以制成电阻率比硅、锗高3个数量级以上的半绝缘高阻材料，用来制作集成电路衬底、红外探测器、光子探测器^[6]。时间来到20世纪90年代之后，半导体材料得到了更加长足的发展，人们相继发现氮化镓、碳纳米管、二维石墨烯等性质更加优秀的半导体材料^[7-8]，这些半导体材料成果对于现代电子信息技术、现代光学探测等多个领域都起到了积极推动的作用。

半导体是通过向基底材料（比如硅、锗等四价材料）掺杂最外层电子数不同的杂质原子而产生性能不同的新材料。掺杂三价元素（如硼）的，整体呈现出少电子的状态，称为P型半导体。反之，掺杂五价元素（如磷）的，整体呈现出多电子的状态，称为N型半导体。将两种半导体粘接，就得到了P-N结。P-N结在我们日常使用的电子器件中应用的十分广泛，而决定P-N结物理状态和相关参数的一个重要因素就是半导体中掺杂的杂质的分布情况，本文希望可以通过电容电压的方法(CV法)对这一重要分布情况进行较为精确地测量，以便于我们加强对于半导体结构和性质的理解。

理论基础

P-N结能够自发地产生电势差，且结上积累的电荷量与施加在结两端的电压有关。这种性质需要使用固体物理的知识解释。如图1是P-N结交界处耗尽层内的电场示意图，耗尽层没有自由电子，故不导电，电荷在耗尽层两侧积累，并产生势垒电压。当施加在结两端的电压增大时，电荷量增加，耗尽层厚度增加，电容减小。设结两端的掺杂浓度分别是和，对应耗尽层厚度是和。在我们的假设中有和。

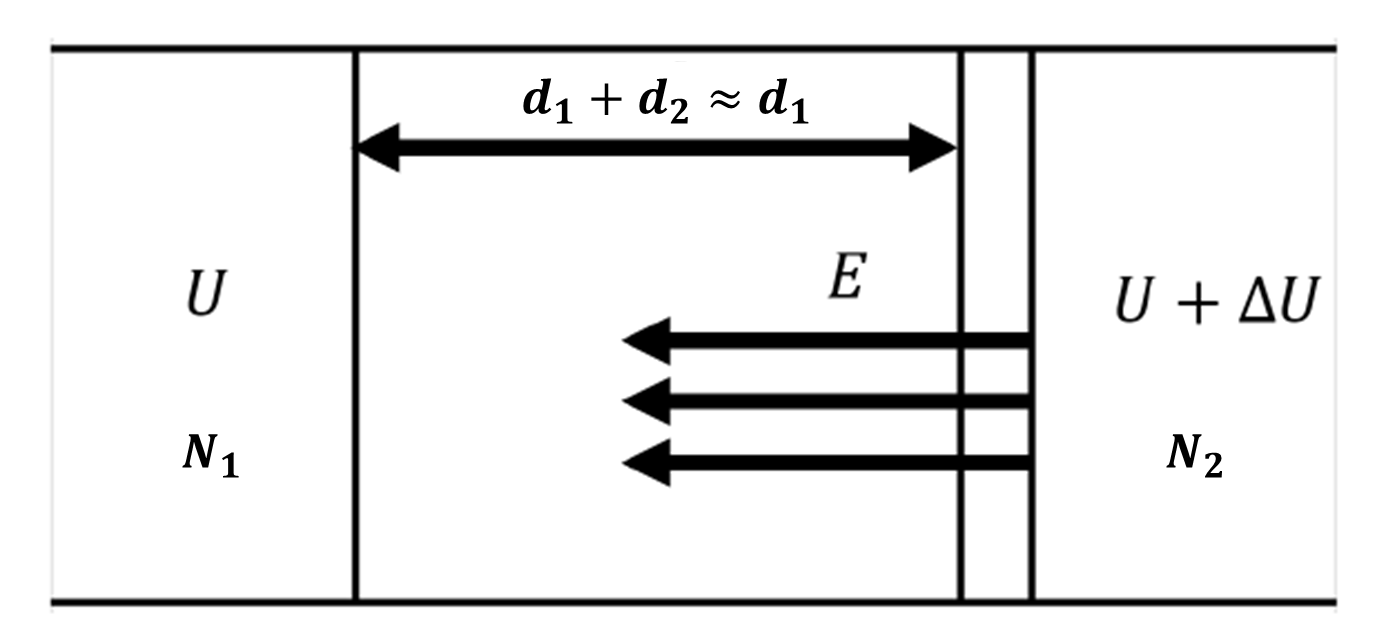
图1：耗尽层电场示意图

设半导体材料介电常数，其中为真空中的介电常数，为半导体材料的相对介电常数，电子电量，积分得到用偏置电压表示耗尽层中存储的电荷量：

$$Q=AdN_2e=A\sqrt{2\epsilon eN_2(V_R+V_D)}$$

其中是P-N结本身由于化学势差而自发产生的电势差，称为自建势。是P-N结截面积，也就是说P-N结中储存的电荷量只是偏置电压的函数。基于这样的观点，可以把P-N结看作一个电容。计算电荷量对电压的偏分，将这个物理量定义为“微分电容”:

$$C=\frac{\partial Q}{\partial V_R}=A\sqrt{\frac{\epsilon eN_2}{2(V_R+V_D)}}=A\frac{\epsilon}{d}$$

这就是说，当偏置电压发生增加时，耗尽层与半导体层交界上的电量会堆积在该界面上，同时耗尽层厚度增加。在不同的偏置电压下，耗尽层厚度不同，所以得到的电容也不同。将上式做变换：

$$\frac{1}{C^2}=\frac{2(V_R+V_D)}{A^2e\epsilon N_2}$$

上式表明和之间存在线性关系。通过回归计算得到系数，从而可以间接测量出轻掺杂一侧的平均掺杂浓度。当空间电荷量发生改变时，单位面积上的空间电荷量发生变化，就能得到的分布函数：

$$N_2(x)=\frac{2}{e\epsilon A^2}\frac{1}{\frac{d(1/C^2)}{dV_R}}=-\frac{1}{e\epsilon A^2}\frac{C^3}{dC/dV_R}$$

相比于传统方法，如四探针和霍尔效应，对于掺杂不均匀的材料难以测量，必须采用破坏性手段。而本实验采用的CV法不必破坏，就能更简便地求出轻掺杂一侧的杂质浓度和分布。需要指出的是，本实验中得到的电压较为微弱，可以使用锁相放大器进行处理，去除噪声，提高信噪比，使得测量更精准。

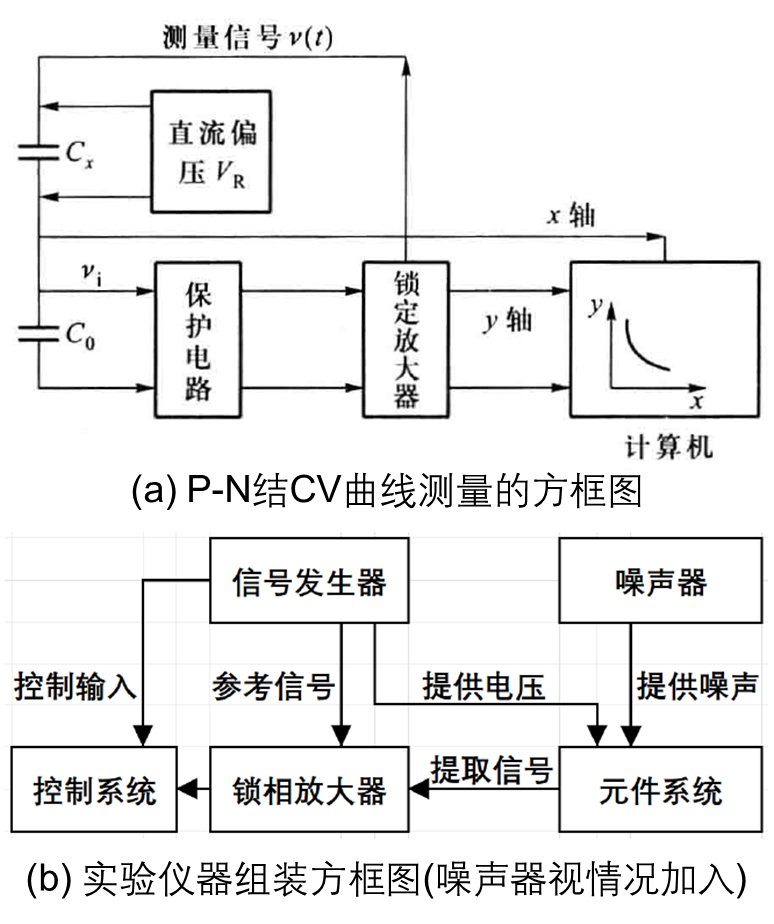
实验仪器及实验装置的组装

如图2(a)中给出了使用CV法测量时实验仪器的连接方框图，(b)中给出了在本实验中所使用到的仪器模块，各模块间的连接和通讯关系用线段表示。下面我们先介绍实验中使用的仪器的原理。

图2：实验测量的方框图

信号发生器和噪声源

信号发生器是能够按设定向外输出稳定正弦交流信号或稳压直流偏置的电源。在本实验中，需要向元件系统提供直流偏置电压的同时施加交流小信号。在向元件系统输出信号的同时，设备还要向锁相放大器输出完全相同的信号作参考信号。本实验中的变化范围是−10V~0V,交流频率选择。实验配置了一台白噪声发生器，用来模拟伴随信号的测量误差。该系统用三极管将晶体管噪声逐级放大，并在输出端用滑动变阻器调节噪声强度。

锁相放大器

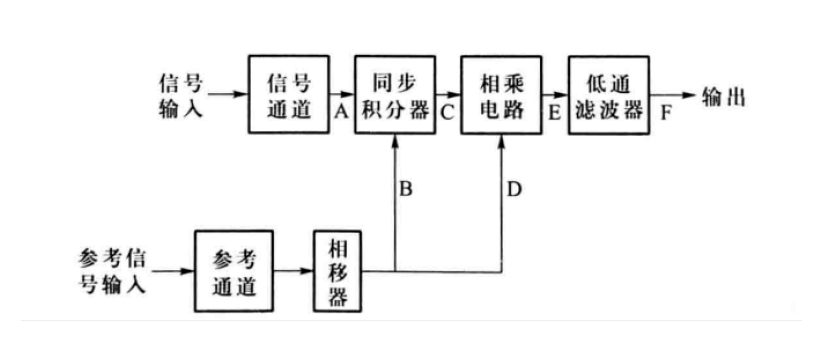
图3：锁相放大器原理图

锁相放大器是一种交流电压表，能精确测定深埋在噪声之中周期重复信号的幅值及相位。具体电路包括：

1. 相敏检波器
   相敏检波器实际上是一个模拟乘法器，输出信号是输入信号和参考信号的乘积，包含差频和和频分量。

2. 低通滤波器
   器件内部噪声包括热噪声、散射噪声、闪烁噪声等。热噪声和散射噪声仅与测量频带宽度有关。可以通过压缩频带宽度减少。闪烁噪声可通过选取适当参考信号频率消除，低通滤波器输出特性为：

   $$\frac{\dot{u}_{sc}}{\dot{u}_sr}=-\frac{R}{R_0}\frac{1}{1+i\omega RC}=-K\frac{1}{1+i\omega RC}$$

   等效噪声带宽为：

   $$\Delta f_N=\frac{1}{K^2}\int_{0}^{\infty}|\frac{K}{1+i\omega RC}|^2df=\frac{1}{4RC}$$

   低通滤波器时间常量越长，则等效噪声带宽越窄。

3. 相关器

   相敏检波器和低通滤波器统称为相关器。考虑输入信号是一埋没在噪声之中的微弱信号：

   $$\begin{cases} V_S=E_i\cos{(\omega_0t+\theta)}+E_n\cos{(\omega t+\alpha)}\\ V_R=E_R\cos{(\omega_0 t)} \end{cases}$$

   经过相敏检波器的过程可以被数学抽象为：

   $$\begin{align} V_0=V_S\cdot V_R=&\frac{1}{2}E_iE_R\cos{\theta}+\frac{1}{2}E_iE_R\cos{(2\omega_0t+\theta)}\\ &+\frac{1}{2}E_nE_R\cos{[(\omega-\omega_0)t+\alpha]}+\frac{1}{2}E_nE_R\cos{[(\omega+\omega_0)t+\alpha]} \end{align}$$

   经过低通滤波器后就会除去大部分噪声：

   $$V'_0=\frac{1}{2}E_iE_R\cos{\theta}+\frac{1}{2}E_nE_R\cos{(\Delta\omega t+\alpha)}$$

4. 同步积分器

   同步积分器是以参考信号频率为参量的方波匹配滤波器。与相关器区别在于同步器积分器输出一个与参考信号同频的方波信号，而相关器输出直流信号。

5. 锁相放大器原理图

   如图3所示为单通道锁相放大器的原理示意图。其中，相移器的作用是改变已知参考信号的相位，通过相关器输出信号，确定待测信号振幅和相位。
   综上所述，对于频率不等于信号频率的噪声理论上都将被消去，只保留了我们需要的信号，从而提高了信噪比。当然这种分离是以时间为代价的，积分时间越长，仪器滤波的品质因数就会越高，分离的信号含杂质波的量就越少，实验越精确，实验中需要考虑时间成本选择合适的积分时间。

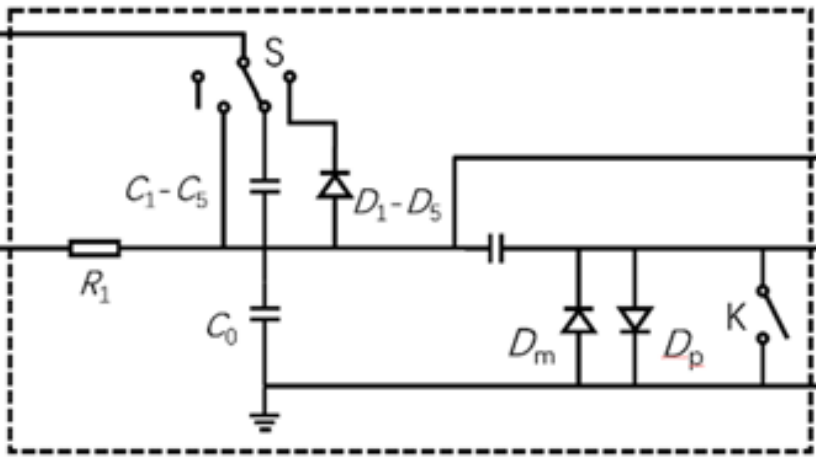
元件系统

实验中将待测的5个二极管和5个标准电容集成在了该装置中，通过旋钮可以选择接入电路的部分，或者将待测元件短接。

图4：元件系统电路图

采用串联分压的方法，利用电容上分压反比于电容的原理，只要测量标准电容上的分压就能算出势垒电容。实验中电容至的值分别是20，40，60，80和100，标准电容为47，待测电容约为50。

显示和控制系统

控制和显示系统包括示波器和电脑。示波器能够实时显示噪声和信号混合后的波形，电脑通过和锁相放大器交换数据的方式控制测量。利用电脑上编写的数据采集程序，开始测量后自动得到结果和图像。

实验操作

研究锁相放大器功能

打开示波器、锁相放大器、噪声器开关，打开电脑。通过按键设定信号初始状态为、内部参考、正弦信号、输入、滤波。
将直流偏置、交流信号接入元件系统，调整旋钮短接待测元件。此时交流信号直接加在两端，在输出端得到的等于输入信号。分别在示波器和锁相放大器上得到这一信号的频率、幅度和相位。
将噪声器用三通接头和测量信号共同接入示波器和锁相放大器，调节白噪声强度，观察示波器上的波形和放大器上输出值的波动情况。改变锁相放大器的积分时间，观察输出信号稳定性的变化，再用程序测量关于t的变化曲线。

电容-电压测量

改变接入电路的电容，观察上分压和相位的变化，确认放大器输出与被测电容间的线性关系。选择合适的积分时间和量程(具体参数会在第五节声明)，设置起止偏置电压及其步长，测至的C-V曲线。

倍频测量

挑选一个没有反向漏电的二极管，设置起止信号电压，确认放大器二倍频输出与信号电压间的平方正比关系。根据得到的倍频数据，选择合适的信号电压，设置起止偏置电压，测量二倍频信号和偏置电压之间的关系。

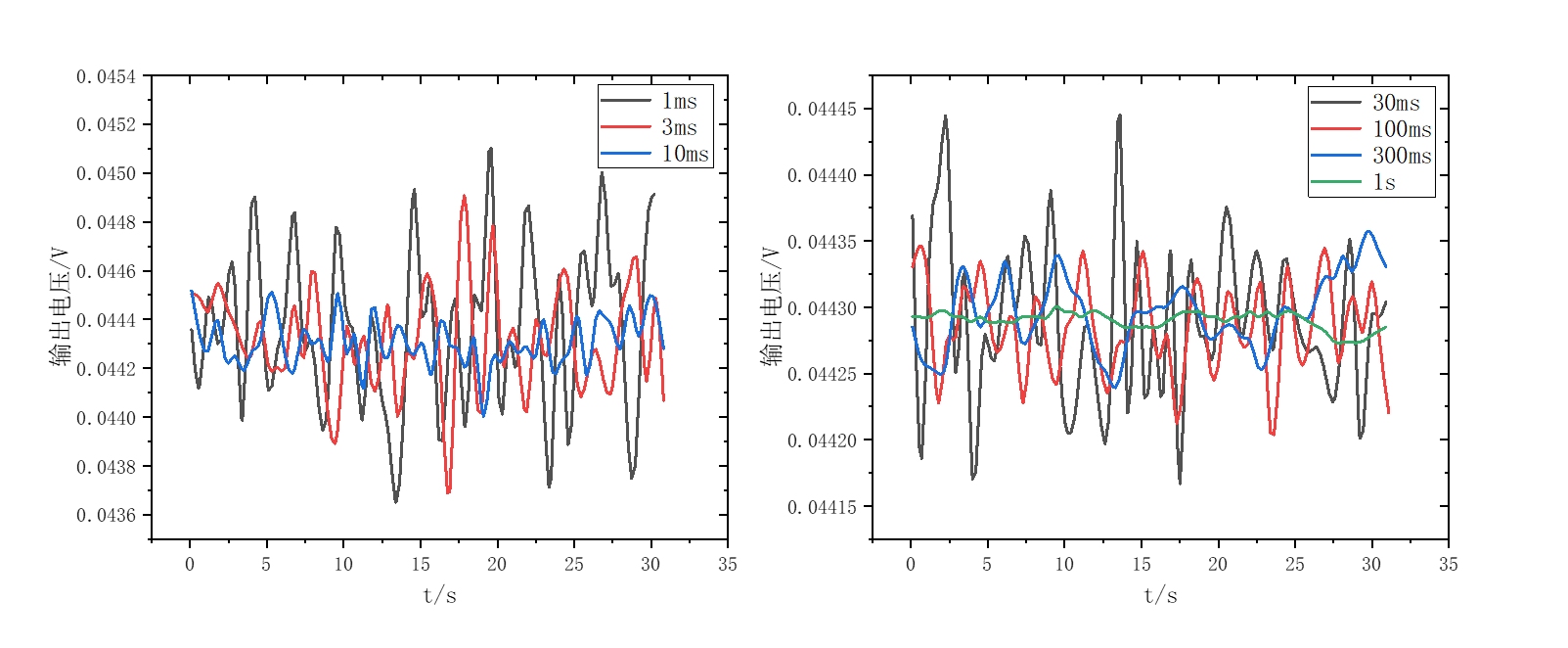
实验数据和分析

研究锁相放大器功能

对于锁相放大器输出的标定有效值为0.05V的正弦波，直接接入示波器后使用CURSOR功能进行测量得：

$$V_{pp}=132mV~~~~~~V_{so}=V_{pp}/2=66mV~~~~~~~f=1.333kHz$$

而通过锁相放大器读出得值为：

$$\overline{V}_{S}=46.40mV~~~~~~\phi_0=18.18°~~~~~~~f=1.333kHz$$

其中，是输出波函数得峰峰值，为输出信号的峰值，为输出信号的频率，为输出信号的有效值，其值应和峰值有关系，为输出信号的初始相位，其实就是锁相放大器自身输出和输入的相位差。

可以看到，示波器测量的结果和锁相放大器测量的结果是相似的，二者差距已经小于示波器波形荧光线本身宽度带来的不确定性，可以认为两种测量结果相同，锁相放大器工作没有问题。

下面我们引入噪声，逐渐增大噪声的强度，观察示波器上的波形和放大器上输出值的波动情况，如图5所示，ABCD依次增大噪声轻度，可以看出波形逐渐变模糊，信噪比降低，信号可辨认性变差。

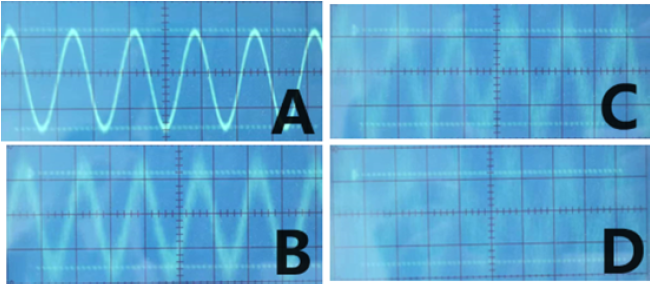
图5：不同噪声下示波器波形图

改变锁相放大器的积分时间为1、3、10、30、100、300和1000ms，观察输出信号稳定性的变化。发现随着积分时间的增加，锁相放大器上读数的更新频率降低，读数的稳定性增加。用程序测量锁相输出关于时间的变化曲线，选取Delay为对应积分时间或直接设置成1s即可(因为这里我们只想观测输入值的稳定性，没有必要等待测量值稳定)

图6：不同噪声下示波器波形图

如图6所示，由于积分时间差距太大时，后面的曲线变化不明显，所以我们将曲线分为两组，左边为1、3、10ms组，其震荡的强度明显大于右边30、100、300、1000ms组。同时，同一组中，积分时间越长，震荡的程度也就越小，即测量结果的稳定性高。

使用图像只能定性的衡量输出信号的稳定性，我们现来定量讨论锁相对噪声的抑制能力。当我们进行多次测量时，衡量数据稳定性的方法是计算这组数据的方差，我们给出这7组数据的方差如下表1所示：

积分时间(ms)	1	3	10	30	100	300	1000
方差	11173	4455	1018	357	116	75	4.2

表1：特定锁相放大器的积分时间对应的一组数据的方差

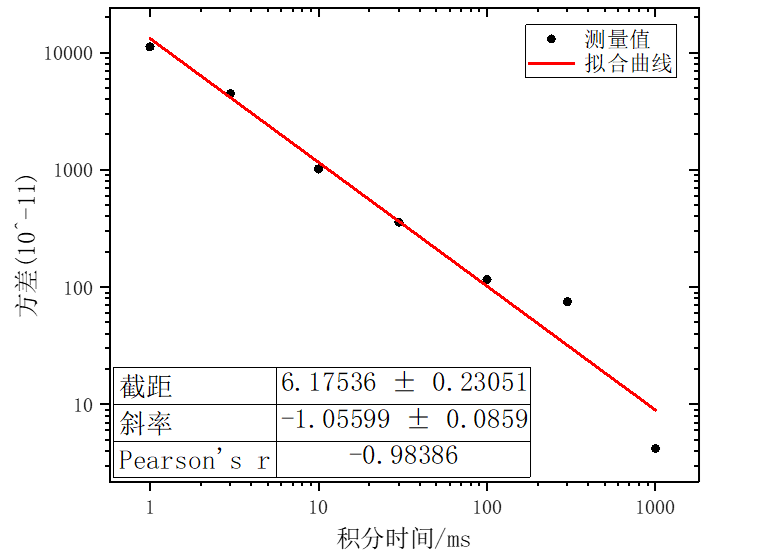
对于实验中引入的白噪声，可以认为其在各频段的强度分布是均匀的。将频带内的每个间隔看作是周期振荡的三角函数，彼此独立取值。因此取长时间的平均可以得到振幅满足：

$$\overline{A^2}=\overline{\sum_i\sin{(\omega_it+\phi_i)}^2}=\sum_i\sin^2(\omega_it+\phi_i)\propto\Delta$$

其中，为通频带宽。通过采样定理，通频带宽应反比于锁相放大器的积分时间。所以，测量数据的波动性（也就是方差）反比于积分周期。如图7所示，我们将坐标轴取对数后进行线性拟合，得到的线性拟合斜率接近-1，所以方差和积分时间成反比从理论上和实验上都是成立的。

图7：锁相放大器积分时间和测量方差的对数拟合图

电容-电压测量

用定值的电容做预实验验证电路可靠性

转动电路元件旋钮分别至，将五个不同容量的电容代替二极管接入电路，通过锁相放大器读出电压输出值和相位角，如下表2所示。

电容	20	40	60	80	100
电压	23.1	43.7	62.0	79.3	95.9
相位	43.46	43.19	43.01	42.89	42.64

表2：锁相放大器输出电压和相位随接入电容的变化

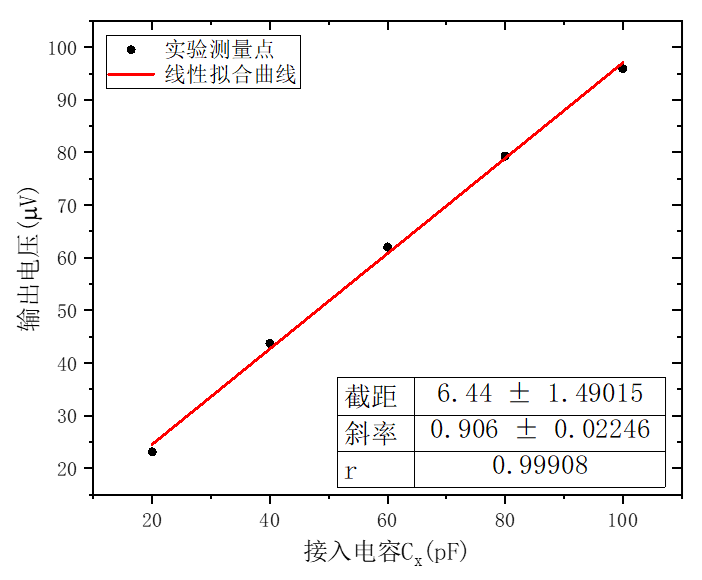
从表2中可以看出，接入电容和输出的电压具有一定的线性关系，拟合图如图8所示。

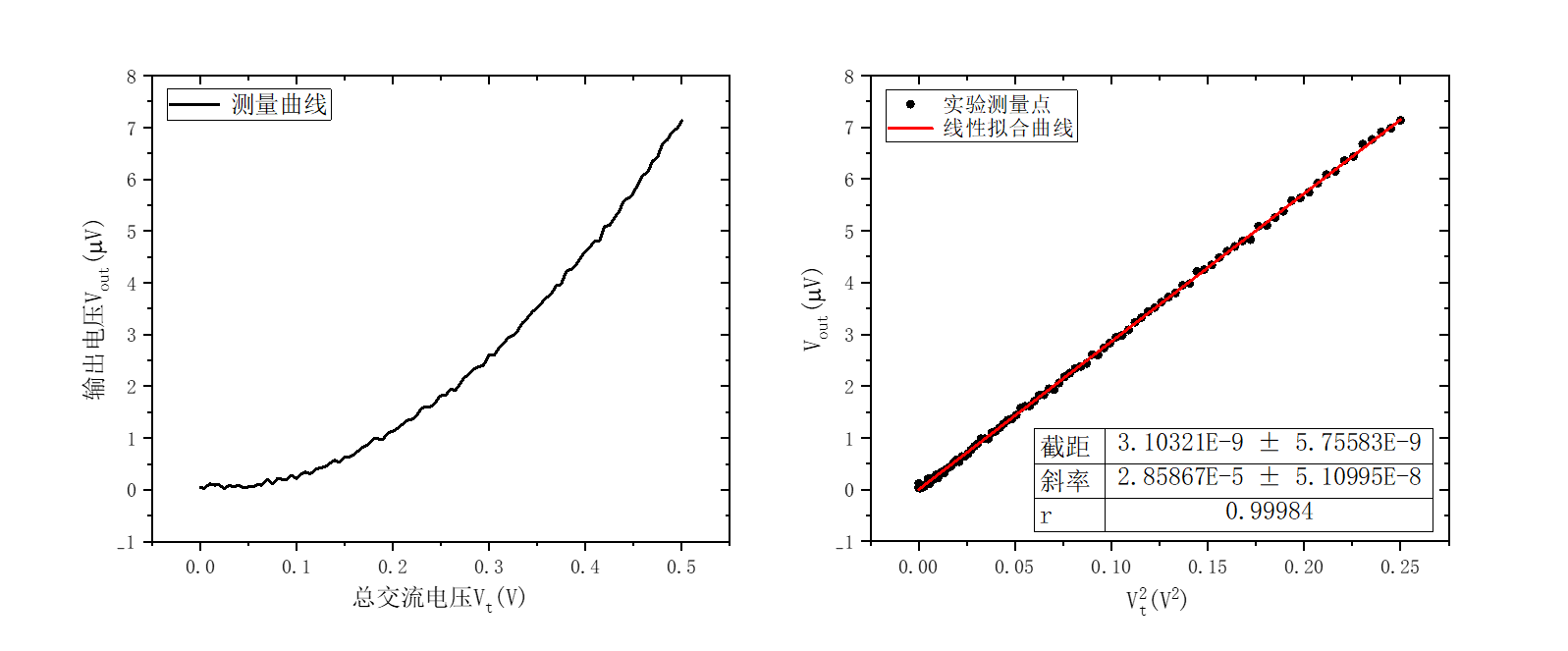
图8：输出电压和接入电容的线性关系

图8给出了具体的输出电压和接入电容的线性关系：，通过图2(a)给出的电路图，我们可以理论上计算出这一关系：

$$V=\frac{V_t}{C_0}C_x \label{eq14}$$

其中，是输入电压，由锁相放大器中读出值为46.33mV，所以理论上给出的斜率为，这值和上面给出的斜率的实验值十分接近。
另一方面，理论上曲线应该是没有任何截距成分的，但是考虑到仪器电容的存在，在电路断开时，仍然可能有分压在仪器电容上，实验中我们标定这个值为，可以看出这个值和上面拟合曲线的截距参数也十分符合。从中我们可以解出一起电容的大小：

$$C_E=V_0/k=7.1pF$$

其中，和分别是拟合曲线的斜率和截距。
另一方面，理论上由方程(14)给出的输出电压的相位应该时完全相同的，但实验结构给出的相位却是变化的，我们给出一下模型进行解释(这个模型也可以解释为什么当很大时，锁相放大器给出的断路有效值不再等于)。

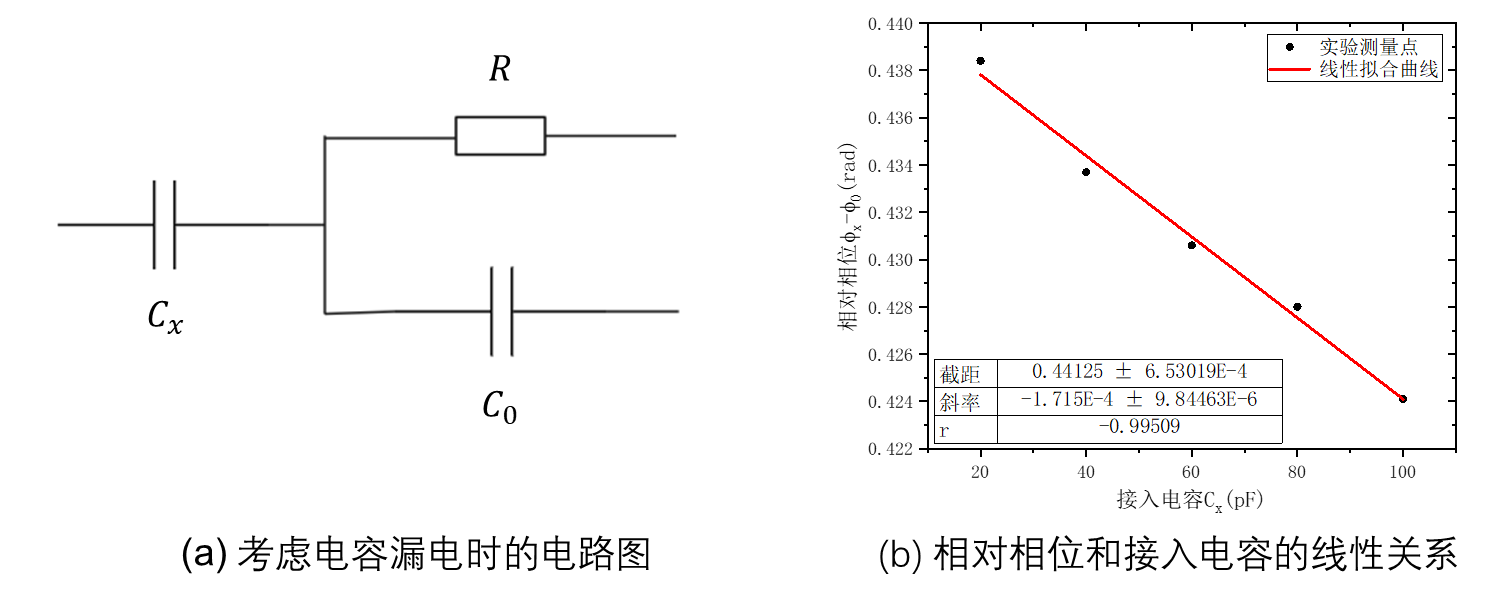
图9：考虑电容漏电时的电路图

如图9(a)所示，我们认为标准电容是有漏电的，也就是存在一个电阻并联在的两端，我们再次计算给出近似的输出电压随接入电容的变化关系：

$$\tilde{V}=\frac{C_xV_t}{C_0+C_x-i/\omega R}$$

因此有相位变化定量值为：

$$\Delta\phi\approx-\omega R\sin^2\phi_0\Delta C_x$$

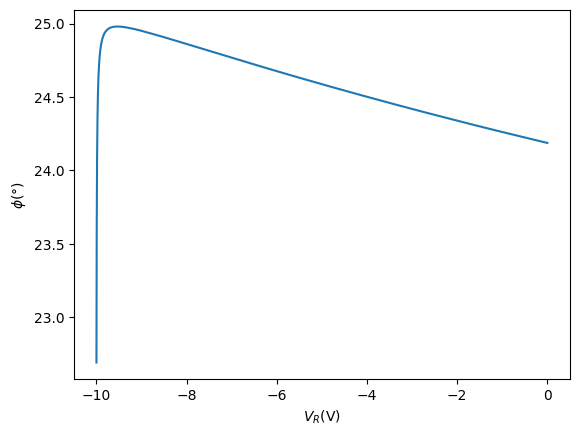
可以看出相对相位和接入电容是近似的具有线性关系的，其中斜率可以给出这个漏电电阻的近似值，。

CV法测量P-N结的掺杂曲线

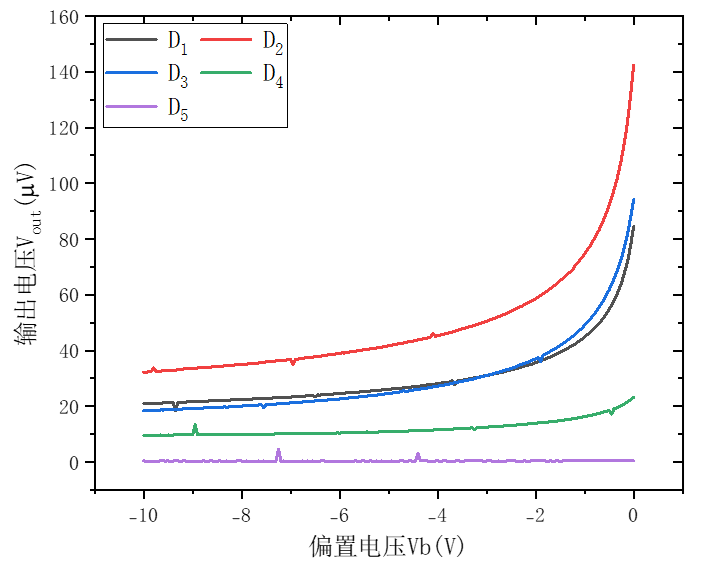
图10：不同P-N结的电压-偏置电压曲线

设置积分时间为100ms，采样点的Delay为1s，锁相放大器探测电压的灵敏度为200V，偏置电压从0V开始到-10V进行扫描，分别测量至的C-V曲线，实验结果如图10所示。注意到图中就是直流偏置电压，也就是前面理论部分提到的，按照我们之前的理论推测，得到的曲线应当呈现出的形式，对比图中的曲线形式，说明我们所有P-N结在反向偏置不大于10V时都正常工作，没有出现大量漏电现象。实验图像中曲线出现了部分毛刺现象，我们在Supplement B中对这一现象做了简单的讨论。
通过图10，我们还可以知道，尽管都可以正常工作，但是的电容值过于小了，尤其是，其噪声值可能都已经大过信号本身的值了，如果继续对其进行测量，我们必须增加积分时间，这样就必须增大测量时间，为了后续研究方便，我们只对前3个P-N结进行完全的讨论，在后续二倍频的讨论中，我们只对电容最大的进行研究，这样我们可以更加明显地发现物理规律。

下面我们首先验证输出电压与反向电压的理论关系是否吻合。对、和作关系曲线，注意计算P-N结电容的公式为，为仪器的电容。

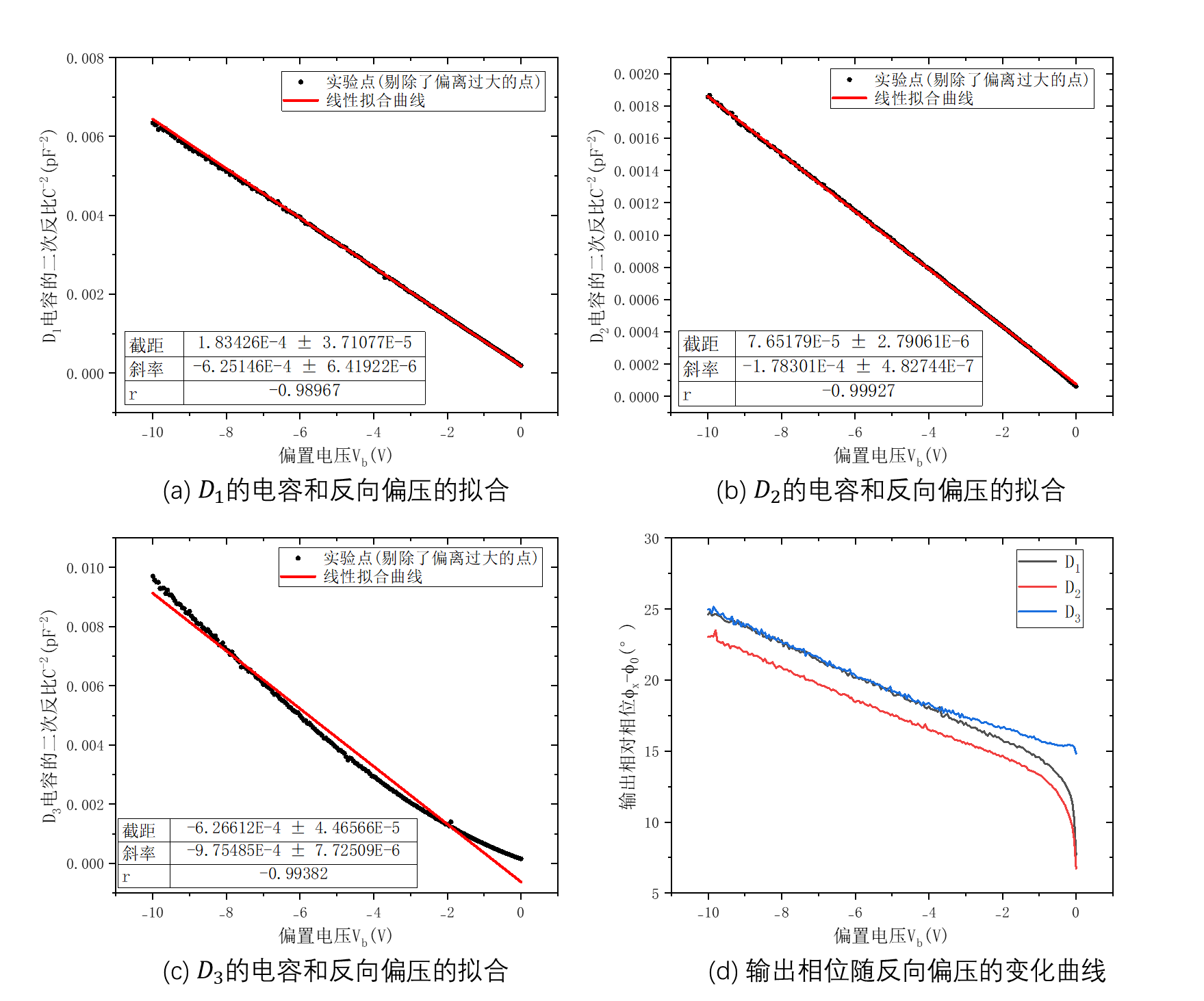
图11：(a)(b)(c)分别为二极管D₁,D₂,D₃的C⁻²-V_b关系曲线；(d)为三者的输出电压的相位随反向偏压的变化

图11(a)(b)(c)分别给出了三种P-N结的电容-反向电压关系式：

$$\frac{1}{C_i^2}=k_i(V_b+V_D)=k_iV_D+b_i$$

表示第个P-N结的关系，根据前文所述，对于每一个，都会有一个对应的掺杂浓度和自建势，它可以方程(19)给出。

$$\begin{cases} k_i=\frac{2}{A^2\epsilon eN_i}\\ V_Dk_i=b_i \end{cases}$$

利用书^[9]中给出的参数()，我们可以分别解出三个P-N结的掺杂浓度和自建势，具体值如表3所示。

P-N结名称	掺杂浓度	自建势
D1	3.80	0.293
D2	13.32	0.429
D3	2.44	0.642

表3：D₁,D₂,D₃的掺杂浓度N和自建势V_D

接下来我们来讨论与的关系,根据前面对于定值电容相位测量时的讨论，相位的变化一般情况下来源于电容的漏电。首先在总的走势上，很符合我们前面图9中所描述的变化，说明相位的改变主要来自于辅助电容的漏电。对于结尾处相位的快速变化，可能是因为没有反向偏压时上电压过大导致漏电效应剧烈的增强。

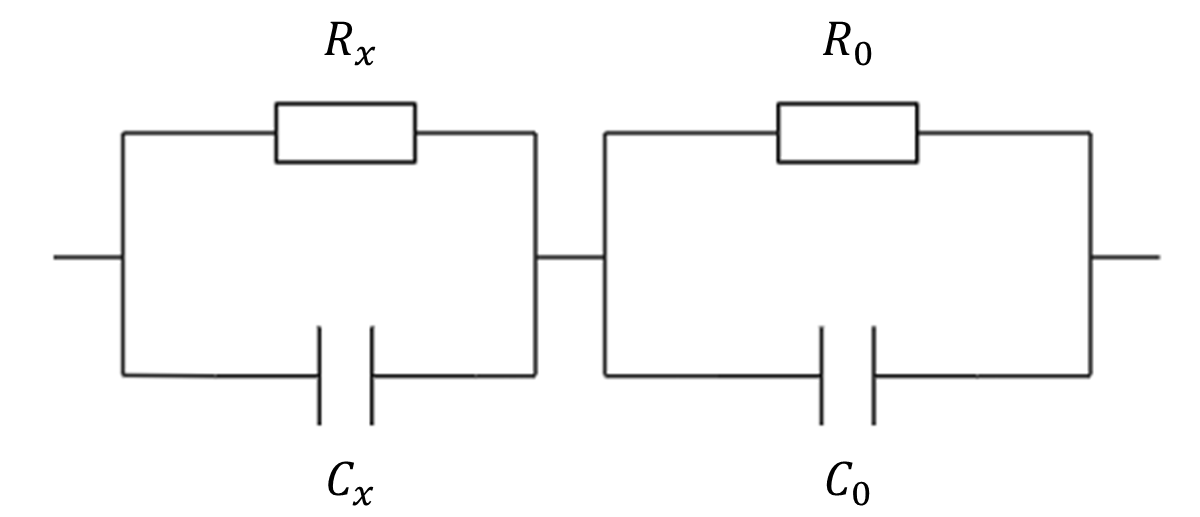
图12：P-N结和标准电容在漏电时的等效电路

当然，P-N结作为电容，也会出现漏电的现象，只不过我们的仪器中在-10V的偏压以内没有出现太强烈的漏电的情况，同样的，如果出现漏电，我们仍然可以将其等效为电阻串联的形式，如图12所示，给出输出复电压和测量复电压得比例关系为：

$$\frac{\tilde{V}_{out}}{\tilde{V}_t}=\frac{R_0(1+j\omega C_xR_x)}{R_x+R_0+j\omega R_0R_x(C_x+C_0)}$$

这将给出相对相位为：

$$\phi=\arctan(\omega C_xR_x)-\arctan\frac{R_0R_x\omega(C_0+C_x)}{R_x+R_0}$$

当时，相对相位可以写成：

$$\cot\phi=-\omega R_x(C_x+C_0)$$

得到了一个和前文中所述的很相似的式子，只不过这将是一个上升的曲线，值得说明的是，式中可能是一个变化的值。当P-N结漏电效应更主导时，相位就会出现随偏置电压减小而减小的情况，此时P-N结出现漏电。如图13所示，我们从理论上给出了考虑P-N结漏电时相对相位的变化曲线，他会呈现出先上升后下降的趋势。当然为了简化计算，我们没有考虑电阻的变化，如果不出现电压过大时，电阻一般变化不大，所以图给出的曲线在边界上可能并不太符合实际情况，但在中间部分和实际相符。

图13：在图12的模型下使用python脚本模拟得到的考虑P-N结漏电时相位的变化图

最后，我们将从前面的结果中推出掺杂曲线，我们这里以为例进行计算，结合：

$$\begin{cases} w=\left[\frac{2\epsilon}{eN}(V_D+V_R)\right]^{1/2}\\ N(w)=-\frac{1}{e\epsilon A^2}\frac{C^3}{dC/dV_R} \end{cases}$$

对数据进行处理，首先求出，后面根据公式分别求出并绘制杂质分布曲线，结果如图14所示。

图14：利用一阶微分值求出杂质分布曲线

倍频测量

锁相可以锁定在参考信号频率的任意次倍频上进行测量。二倍频信号可以视为基频信号对激励信号的的微分。因此通过测量二倍频信号，可以直接测量基频信号的微分，精度往往可以比对基频信号直接进行数字微分高很多。其原理可以用IV曲线来理解。通常来说，样品上的电压降是施加的激励电流的函数。样品电阻为。我们在样品上施加一个直流偏置电流，然后对在附近做泰勒展开并变形，有:

$$V=V_{dc}+f'I_0\sin\omega t+\frac{f"}{2}I_0^2\frac{1-\cos2\omega t}{2}+\cdots$$

实验中，保持偏置电压为−5V不变而取信号电压为0~500mV,测量倍频信号和信号
电压的关系作图，如图15。可以看出在信号电压不至于很大（小于500mV）的条件下，理论得到的平方正比关系是基本成立的。

图15：倍频信号和信号电压的关系图

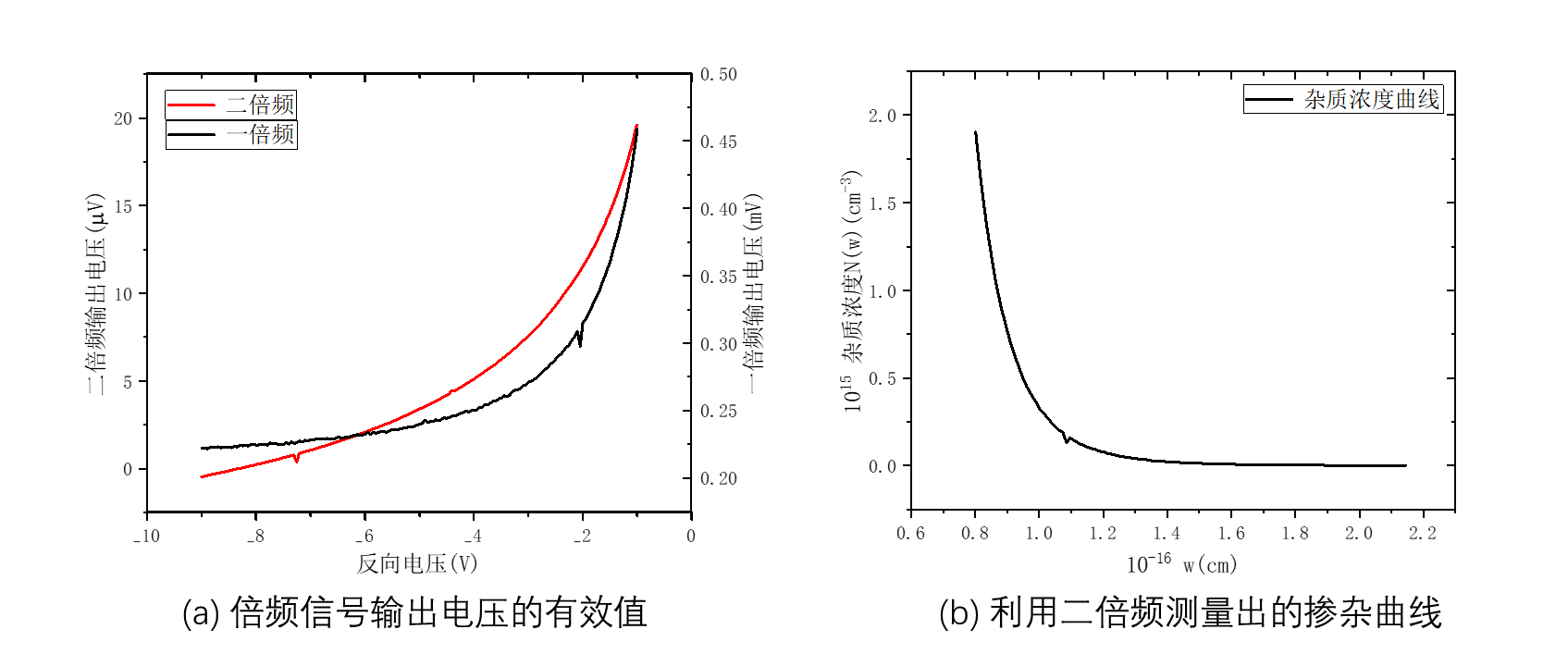
另外，在进行杂质分布测量时，除了利用一倍频，也就是上面所述的方法进行测量外，我们也可以利用二倍频来测量。在二倍频测量的实验中，我们选择了信号电压，偏置电压变化范围为−1V~−8V。使用一倍频微分方法和二倍频方法，分别可以得到杂质随结深的分布曲线，转换关系是：

$$\frac{dC}{dV_R}=\frac{2V_0}{V_2^2}$$

其中，是一倍频输出时的电压值，是二倍频输出的电压值。这样可以直接代换方程(23)，求出掺杂分布，结果如图16所示。

图16：利用二倍频对掺杂浓度进行测量

若将图16(b)和图14(b)画在一起，两者的值还是非常接近的，所以说明我们的测量没有问题。由于信号的测量在高偏压区值很小，会严重受白噪声的影响，测量得到的数据有明显的波动。在这种情况下，贸然使用相邻点间的差分方法计算会让数据波动很大，甚至会出现噪声值大于测量值，导致微分值为负数。而使用二倍频测量法，不需要取微分，则能很好地避免这个问题。

结论

本实验在理解P-N结原理的基础上，设计了通过电容-电压法测量P-N结各处杂质浓度和自建势的实验。对于实验中难以测量的微弱物理量，验证了锁相放大器对于与参考信号同频的信号的放大能力。我们发现状态良好的P-N结各深度处的杂质浓度基本一致，差异微小。同时，我们深入研究了锁相放大器的降噪能力与积分时间的定量关系，并设计实验加以证明。

参考文献

[1] 黄昆,韩汝琦. 半导体物理基础:第190卷[M]. 科学出版社,1979.

[2] SIFFERT P, KRIMMEL E. Silicon: evolution and future of a technology[M]. Springer Science & Business Media, 2013.

[3] ASBECKPM,NAKAMURAT. Bipolartransistor technology: Past and future directions[J]. IEEE Transactions on Electron Devices, 2001, 48(11): 2455-2456.

[4] NING T H. History and future perspective of the modern silicon bipolar transistor[J]. IEEE Transactions on Electron Devices, 2001, 48(11): 2485 2491.

[5] BLAKEMOREJ. Semiconducting and other major properties of gallium arsenide[J]. Journal of Applied Physics, 1982, 53(10): R123-R181.

[6] 百度. 砷化镓[EB/OL]. 2024. https://baike.baidu.com/item/%E7%A0%B7%E5%8C%96%E9%95%93/643608.

[7] RAIS-ZADEHM,GOKHALEVJ,ANSARIA,etal.Galliumnitrideasanelectromechanicalmaterial[J]. JournalofMicroelectromechanicalSystems, 2014, 23(6): 1252-1271.

[8] GEIM AK. Graphene: status and prospects[J]. science, 2009, 324(5934): 1530-1534.

[9] 荀坤吴思成. 近代物理实验(第四版)[M]. 高等教育出版社,2015.

Supplement A：对实验过程和结果的一些解释(对应书中的思考题)

1. 如何正确地选择锁相放大器灵敏度？锁相放大器测得的信号相位是由什么决定的？

   答：锁相放大器在使用中不能超量程，否则会过载甚至损坏。选择尽可能高的灵敏度能增大信噪比，使测量更精准。锁相放大器能够用相移器不断调整参考信号相位，直到参考信号和输入信号的积分值最大，此时调整后的参考信号和输入信号相位一致，相移器的角度改变量就是信号相位。

2. 在使用锁相放大器时，对所提取微弱信号的频率与模拟乘法器中参考信号的频率有何要求？噪声中与参考信号频率相同的成分能否用锁相放大器来消除它的影响？

   答：输入信号的频率应当是参考信号的频率的奇数倍（理想情况下二者应同频）。锁相放大器是一个选频滤波设备，不能过滤与信号同频的噪声。

3. 如果P-N结二极管存在漏电对测试结果会有什么影响?

   答：漏电会影响标准电容上的分压和相位，偏置电压提高后输出电压会变得异常高，相位会急剧降低。

Supplement B: 对于图10中毛刺的讨论

图10中出现了理论无法解释的毛刺，通过实验的方法，我们先后测量两次状态完全相同的，得到如图17所示的曲线。

图17：先后两次状态完全相同的实验结果

通过对比左右两张图可以看出，这种毛刺的出现是完全随机的，比较可能的原因是由于锁相放大器内部老化，出现了短暂短路，使计算的输出电压急剧增加。