摘要： 当两块超导体之间具有弱连接时，库伯对在两超导体间量子隧穿，产生隧穿电流的现象称为约瑟夫森效应。约瑟夫森效应是宏观量子现象的生动体现，目前在灵敏探测、电压基准及量子电路等领域有着广泛应用。本实验使用高温超导YBa₂Cu₃O_7−x，将不同晶向的两块超导材料用超导薄膜粘接，实现弱连接，从而构成双晶约瑟夫森结。实验通过测量双晶约瑟夫森结在液氮温度（77K）下，无微波辐照和有微波辐照两种情况下的伏安特性曲线，观察到了直流和交流约瑟夫森效应。实验对比了双晶约瑟夫森结和同尺寸不含双晶结的超导材料，在超导转变特性、伏安特性上的差异，验证了约瑟夫森效应的存在。通过微波辐照下出现的微波感应台阶，计算出的微波频率理论值与实际值温吻合，进一步验证了约瑟夫森效应理论的正确性。

关键词：约瑟夫森效应，超导

引言

对于一些特殊材料，当温度降低至临界温度以下时，材料体现出零电阻和完全抗磁的特性，这种现象称为超导。超导态于1911年被荷兰物理学家卡末林·昂内斯首次观测^[1]。1933年，沃尔特·迈斯纳和罗伯特·奥克森费尔德发现了超导体的“迈斯纳效应”，即超导体在超导状态下会排斥磁场。随后，伦敦兄弟在1935年提出伦敦方程，用以描述超导体中电流的行为^[2]。伦敦方程的提出帮助人们更好地理解超导体在电磁场中的表现，并且迈斯纳效应也成为判断超导状态的重要标志。1957年，约翰·巴丁、利昂·库珀和约翰·施里弗提出了著名的BCS理论^[3]，该理论解释了超导体中的电子成对形成库珀对，并通过声子中介形成相干态。这一理论成功解释了低温超导体的微观机制。1986年，贝多兹和米勒在钙钛矿结构氧化物中发现了高于40K的超导体^[4]。这一发现开启了高温超导体的研究热潮，并且带来了超导转变温度的新高度。对超导态的研究至今仍是物理学的热门课题。

通常，根据超导转变温度与液氮温度的关系，可以将超导体分为低温超导体和高温超导体。常规低温超导机制已经被BCS理论解释，理论表明临界温度下，费米面附近的电子会因为电声作用而两两结合，形成库伯对，库伯对在超导体中以不衰减的动量传播，从而导致了超导电性。而对于非常规高温超导机制的解释，目前还没有定论。现在已知临界温度最高的超导体转变温度仍远低于室温，因此对室温超导体的探索也一直备受关注。

1912年，英国物理学家约瑟夫森预测了在两块弱连接的超导体间库伯对发生量子隧穿的现象，即约瑟夫森效应。约瑟夫森效应可以在常规尺度下观测，是宏观量子效应的生动体现。目前，约瑟夫森效应在量子线路领域有重要应用，包括超导量子干涉仪、超导量子比特等。

本实验使用高温超导体YBa₂Cu₃O_7−x，将不同晶向的两块超导材料用超导薄膜粘接，实现弱连接，从而构成双晶约瑟夫森结。实验旨在通过测量双晶约瑟夫森结与同尺寸超导材料的伏安特性曲线，验证约瑟夫森效应的存在及其理论正确性，从而加深对宏观量子性的理解；通过对超导特性的观察，加深对于超导电性的理解。

理论

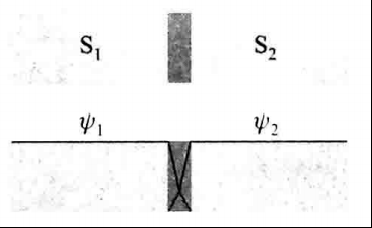
图1：S-I-S约瑟夫森结及结两侧超导体波函数示意图

超导态

超导态是指当超导材料温度降低到临界温度时，材料表现出零电阻和完全抗磁两种特性，其中完全抗磁现象也被称为迈斯纳效应。根据超导材料的机制能否由BCS理论解释，可以将超导体分为常规和非常规超导体；根据转变温度是否高于液氮温度，可以将超导体分为高温和低温超导体。实验表明当穿过超导体的电流大于临界电流或施加在超导体上的磁场强度达到临界磁场强度时，超导态将被破坏。

传统低温超导体的机制可以由BCS理论解释，费米面附近动量、自旋相反的两个电子由于电声相互作用相互吸引称为库伯对，大量库伯对相干凝聚到同一量子态上，导致超导电性的出现。

没有磁场时，超导材料从正常态到超导态的转变为二级相变。根据GL理论，可以用序参量，其中模和相位都是空间位置的实函数，且，是参与配对凝聚的超导电子浓度。对于孤立、均匀的大块超导样品，内部参加库伯对凝聚的超导电子相位相干，则。

约瑟夫森效应

下面分析S-I-S结中的约瑟夫森效应。考虑两块超导体被一绝缘层分开的情况，当绝缘层足够薄时，两超导体内库伯对波函数存在交叠，即两超导体实现弱连接，这样的结构称为S-I-S约瑟夫森结。如图1所示。

设图中超导体中的波函数分别为，。有：

$\begin{cases} i\hbar\frac{\partial\psi_1}{\partial t}=E_1\psi_1+k\psi_2\\ i\hbar\frac{\partial\psi_2}{\partial t}=E_2\psi_2+k\psi_1 \end{cases}$

其中，是超导体的能量，表征二者之间的耦合程度。上式整理得：

$\frac{\partial n_{s1}}{\partial t}=-\frac{\partial n_{s2}}{\partial t}=\frac{2k}{\hbar}\sqrt{n_{s1}n_{s2}}\sin{(\theta_2-\theta_1)}$ $\frac{\partial \theta_1}{\partial t}=-\frac{E_1}{\hbar}-\frac{k}{\hbar}\sqrt{\frac{n_{s2}}{n_{s1}}}\cos{(\theta_2-\theta_1)}$ $\frac{\partial\theta_2}{\partial t}=-\frac{E_2}{\hbar}-\frac{k}{\hbar}\sqrt{\frac{n_{s1}}{n_{s2}}}\cos{(\theta_2-\theta_1)}$

令，则有约瑟夫森第一方程：

$j=j_C\sin{\phi}$

式中即为约瑟夫森电流密度，为约瑟夫森临界电流密度。若和为相同材料，即，又，则有约瑟夫森第二方程：

$\frac{\partial\phi}{\partial t}=\frac{2e}{\hbar}V$

当结两侧电压时，相式(6)位差为常量，记为，则由式(5)，有。这表明当约瑟夫森结两端不存在电压时，仍有直流电流可以无阻通过，此即直流约瑟夫森效应。当时，有，进而由式(5)知。这表明此时结中隧穿电流是频率为的正弦电流，此即交流约瑟夫森效应。

由于正弦电流的时间平均为0，因此无法在直流伏安特性曲线中被观测。为观察交流约瑟夫森电流，可施加微波辐照。设辐照的微波频率为，此时结两端电压为，其中。由式(6)和式(5)，有：

$j=j_C\sin\left(\phi_0+\frac{2e}{\hbar}Vt+\frac{2eu}{\hbar\omega_1}\sin\omega_1t\right)$

上式可改写为：

$j(t)=j_C\sum_{m=-\infty}^{+\infty}J_m\left(\frac{2eu}{\hbar\omega_1}\right)\sin\left[\left(\frac{2e}{\hbar}V+m\omega_1\right)t+\phi_0\right]$

当时，上式右端每一项都随时间正弦振荡，平均值为0。当时，上式项为常数项，平均值非零，因此

$\overline{j(t)}=j_CJ_{-n}\left(\frac{2eu}{\hbar\omega_1}\right)\sin\phi_0=(-1)^nj_CJ_n\left(\frac{2eu}{\hbar\omega_1}\right)\sin\phi_0$

这意味着当时，约瑟夫森电流出现直流分量，在伏安特性曲线上将出现随电流增加而不变的恒压电流，即微波感应台阶。如图2所示。

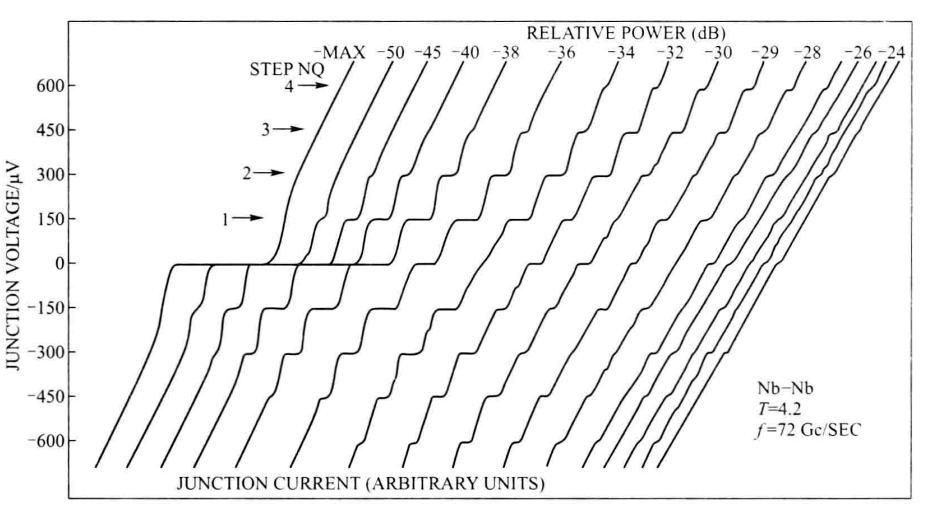
图2：交流约瑟夫森效应伏安特性曲线

约瑟夫森结的类型

实现超导体间弱耦合的方式很多，(a)通过绝缘或普通金属薄膜连接，称为隧道结；(b)一个超导体的尖端与另一个超导体接触，称为点接触结；(c)通过狭窄的微桥连接同种超导材料，称为微桥结。

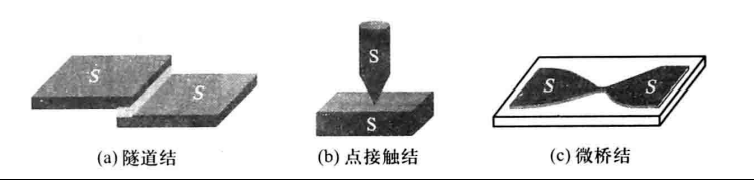
图3：几种典型的约瑟夫森结

本实验使用的是高温超导体。YBa₂Cu₃O_7−x令两块材料在平行于衬底表面方向的晶向不同，并将其粘接在一起。在晶界处，超导电性由于晶格缺陷而被弱化，形成弱连接，构成双晶约瑟夫森结。

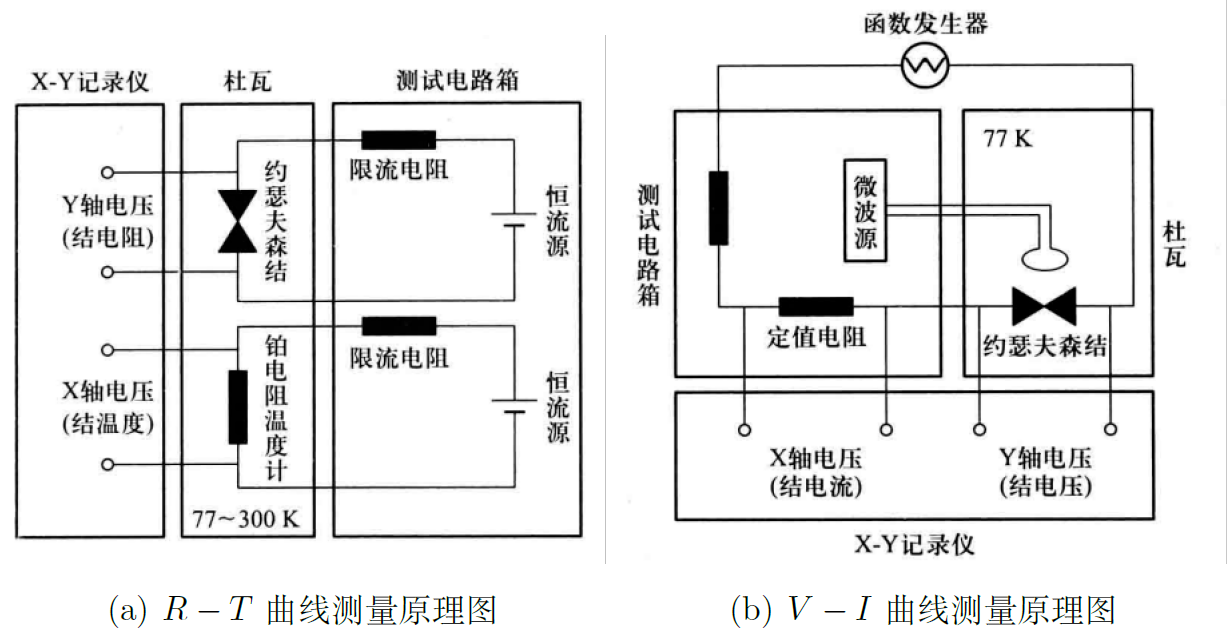
实验

实验装置

本实验的装置依功能可划分为三个部分：测量系统、记录系统和降温系统。如图4所示。

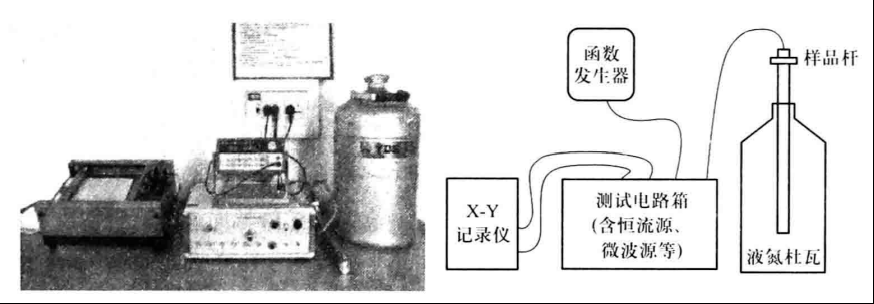
图4：实验装置示意图

测量系统

测量系统包括函数发生器、微波信号源、测试电路箱、样品杆，作用是测量高温超导体的电阻随温度的变化以及伏安特性曲线。其中样品杆上低温温度计为铂电阻温度计，测试电路箱中有恒流源为铂电阻和约瑟夫森结提供直流偏置。

测量曲线时，将铂电阻温度计两端电压和约瑟夫森结两端电压分别作为记录仪的x轴和y轴输入。约瑟夫森结和铂电阻电阻通过电压与恒流源电流计算得到，温度通过对照铂电阻温度计电阻-温度数据表得到。

测量曲线时，用函数发生器输出低频三角波信号，得到准静态的大小连续改变、并可以改变极性的电流。将定值电阻两端电压和约瑟夫森结两端电压分别作为记录仪的x轴和y轴输入。约瑟夫森结上电流通过定值电阻电压和定值电阻阻值计算得出。观察交流约瑟夫森效应时，同时打开微波信号源，便可观测到微波感应台阶。

图5：实验测量原理图

记录系统和降温系统

记录系统为记录仪，可以将输入信号按比例绘制在坐标纸上，用于绘制曲线和曲线。实验过程中也可以用来测量超导材料温度，以确定能否从样品杆中取除超导材料。降温系统为液氮杜瓦瓶，用于将超导样品降至转变温度以下。

实验步骤

由于双晶结样品能能承受的电流较小，要防止静电损伤样品。实验过程中，在调试仪器、连接电路前以及测量完成后都要将测试电路箱调至“短路”状态。同时，信号发生器要缓慢增大幅值，测量完成后要将幅值调至最小再关闭。

本实验中，铂电阻电流为0.9mA，约瑟夫森结电流为50μA。

测量高温超导双晶约瑟夫森结的超导微桥的曲线

将测试电路箱置于“短路”状态，将双晶结样品放入样品杆中，按照图5连接电路，打开测试电路箱和记录仪开关。
将测试电路箱置于“测量”状态，在记录仪适当位置夹上坐标纸，抬起笔尖，将x轴和y轴同时分别置于“zero”和“measure”，观察笔尖在零点和样品常温状态对应数据点的位置。将零点调节至坐标纸左下方；调整分度值，使得整条曲线尽可能铺满坐标纸。
落下笔尖，分别将x轴和y轴中的一个置于“measure”状态，在坐标纸上画出坐标轴。（最好提前观察原点位置，试使之落在格点上，方便后续测量）
将x轴和y轴都置于“measure”状态，放下笔尖，将样品杆伸入液氮杜瓦瓶中记录仪会自动绘制出曲线。实验过程中也可以用来测量超导材料温度，以确定能否从样品杆中取除超导材料。
结合x轴和y轴数据点坐标、分度值和恒流源输出电流大小，可以得到铂电阻和双晶结电阻，对照铂电阻温度计的电阻温度数据表，可以得到温度。据此，确定双晶结的超导转变温度。

在液氮沸点(77K)下，测量双晶结的曲线

将测试电路箱置于“短路”状态，按照图5重新连接电路，并将测试电路箱测量功能切换至状态。
打开信号发生器，输出低频() 三角波。逐渐增加三角波幅值，同时调整记录仪x轴分度值，使笔尖移动范围尽量铺满坐标纸；调小y轴分度值，便于观察何时到达约瑟夫森临界电流。
结合x轴数据点坐标、分度值、恒流源输出电流和定值电阻阻值大小，可以得到双晶结上电流。曲线开始上升点处对应电流即为约瑟夫森临界电流。

在液氮沸点(77K)下，施加微波辐照，测量双晶结的曲线

在上一步基础上，连接微波发生器与样品杆，打开微波发生器输出微波。
调节微波的频率和功率，直到可以观察到明显的台阶。实验中，在微波频率，功率最大时，观察到了明显的微波感应台阶。
结合x轴和y轴数据点坐标、分度值、恒流源输出电流和定值电阻阻值大小，可以得到双晶结上电流和电压。根据感应台阶高度，可以理论计算微波频率，将其与实际值对比，验证约瑟夫森效应的理论预测结果。

最后，用同尺寸的超导样品重复上述操作。对比得到的结果。

实验结果与讨论

电阻-温度特性对比

我们分别绘制了高温超导双晶约瑟夫森结和同尺寸的超导微桥的R−T曲线，通过computer vision的方法将数据点按轴的分度值提取出来，通过spine的方法进行插值，并对数据进行分析。最终的R-T图如图6和图7所示：

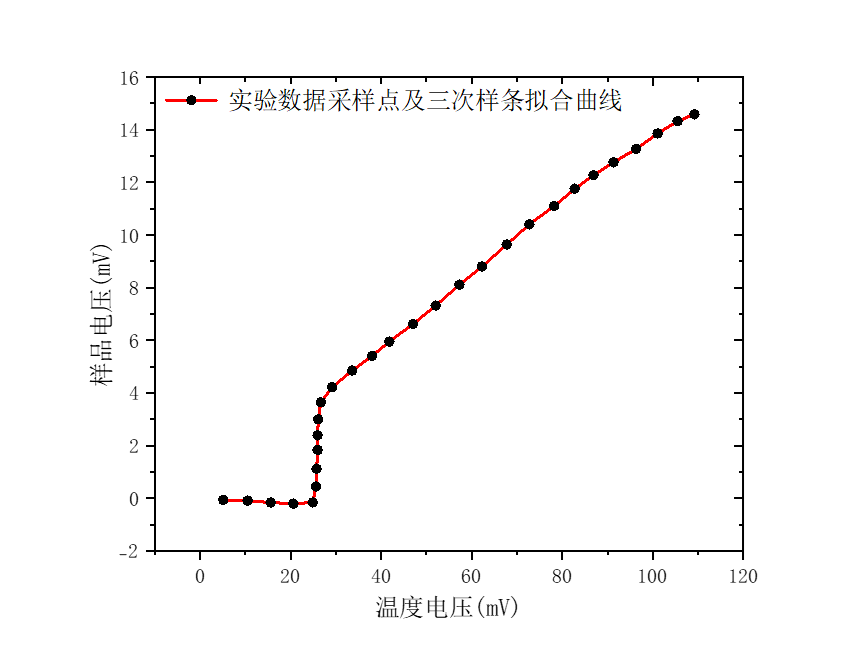
图6：高温超导双晶约瑟夫森结的电阻-温度变化曲线(x轴分度值5mV/cm,y轴分度值1mV/cm)

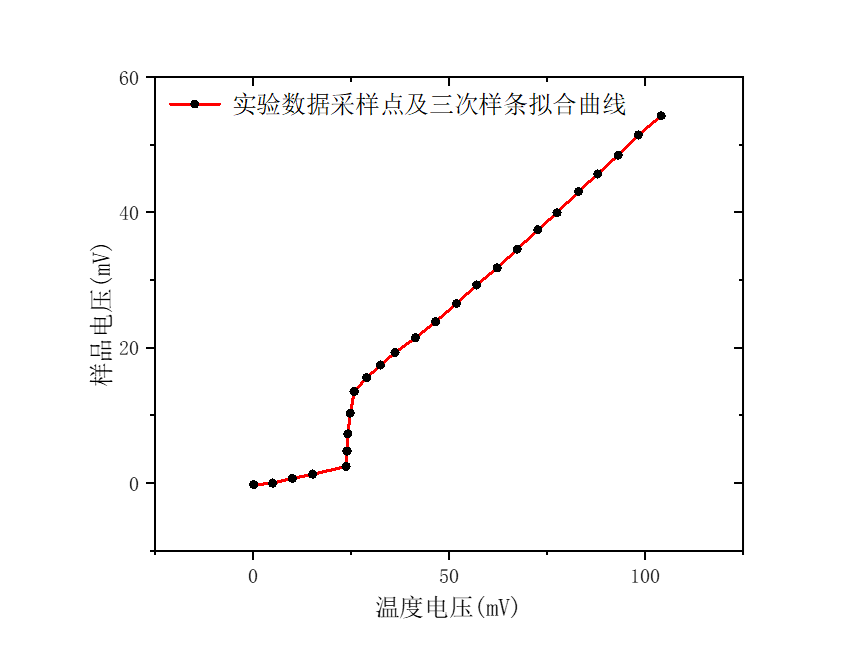
图7：同尺寸超导样品的电阻-温度变化曲线(x轴分度值5mV/cm,y轴分度值5mV/cm)

根据曲线，高温超导双晶约瑟夫森结和同尺寸超导样品转变温度时，铂电阻阻值分别为：

$R_{T,1}=\frac{5.0\times5}{0.9}\approx28\Omega,~~R_{T,2}=\frac{4.8\times5}{0.9}\approx27\Omega$

对照铂电阻的电阻温度数据表可得，二者的转变温度均为。双晶结和超导微桥的电阻-温度变化趋势基本一致，而转变温度又几乎相同，这说明约瑟夫森结中的弱连接不会破坏超导体的相变行为。

伏安特性对比

在没有外界辐射时，观察到直流约瑟夫森效应的伏安特性曲线如图8所示：

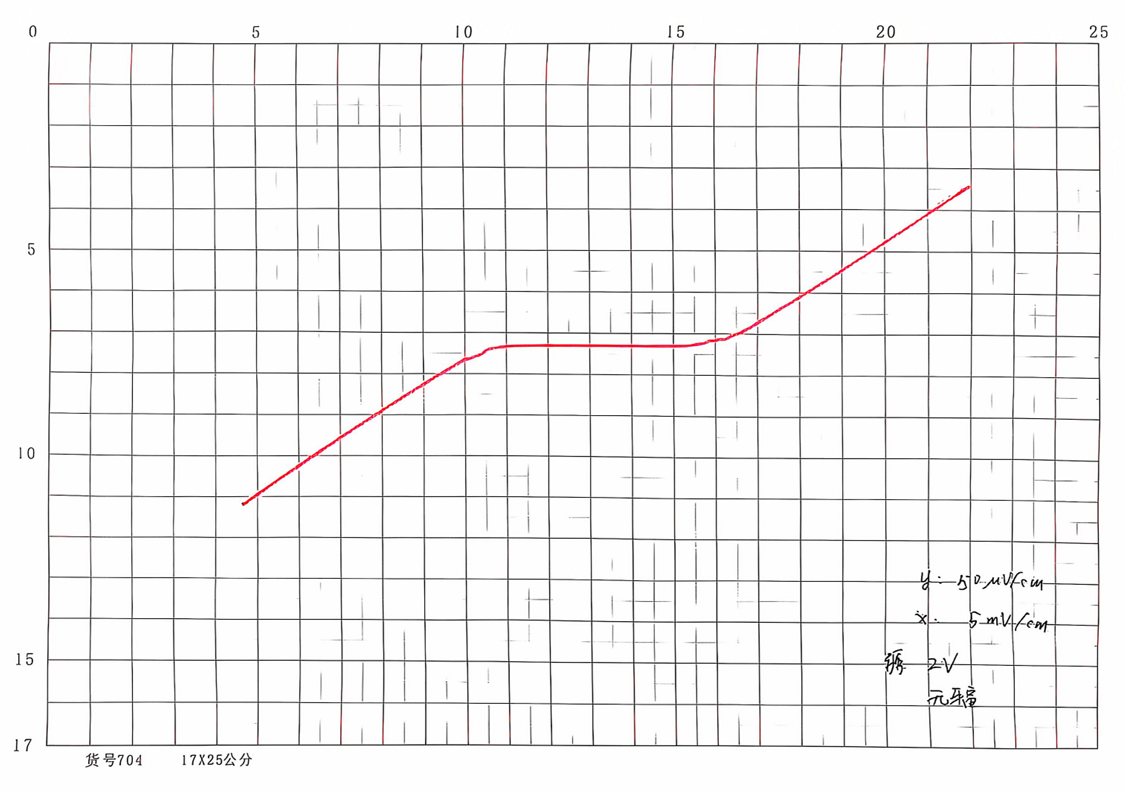
图8：高温超导双晶约瑟夫森结在无微波辐照下的伏安特性曲线(x轴分度值5mV/cm,y轴分度值50μV/cm)

根据曲线，在无微波辐照下的约瑟夫森临界电流为：

$I_C=\frac{5\times5\times10^{-3}}{2\times50}=0.25mA$

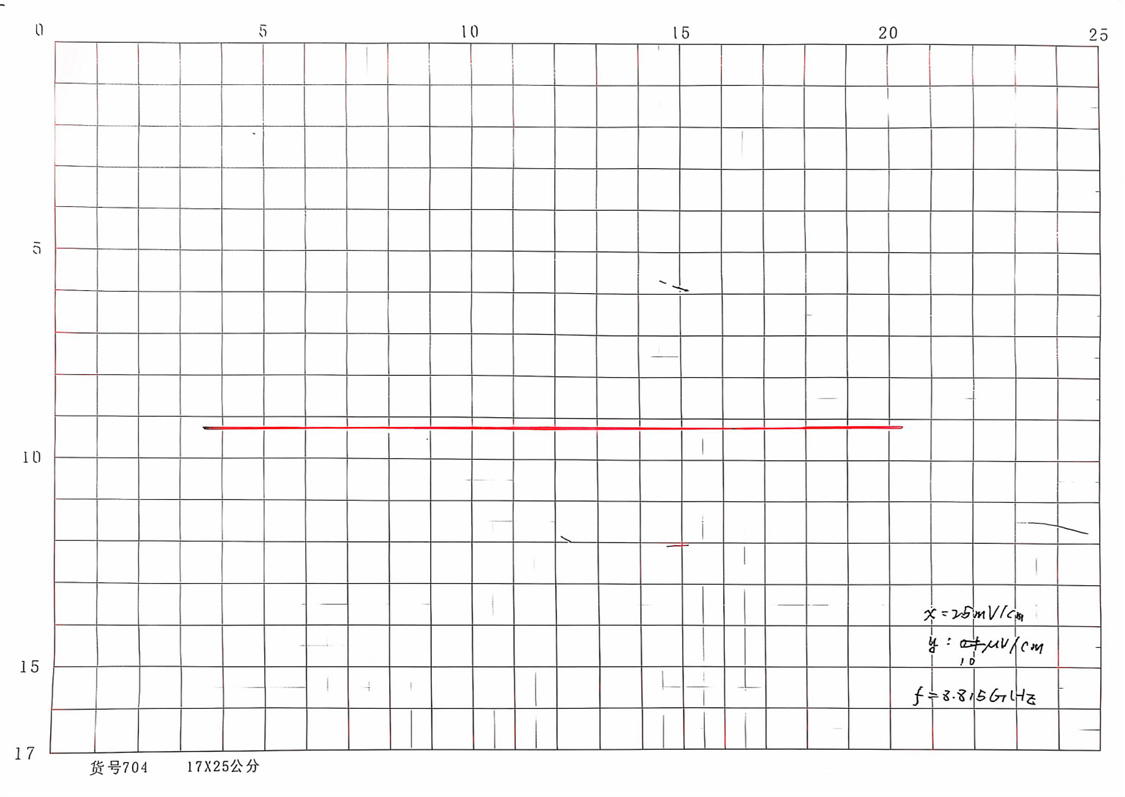
如图，同尺寸超导样品在小功率，频率为的微波辐照下，电压恒为0。

$图9：同尺寸超导样品在小功率微波辐照下的伏安特性曲线(x轴分度值25mV/cm,y轴分度值10$\mu$V/cm)$

图9：同尺寸超导样品在小功率微波辐照下的伏安特性曲线(x轴分度值25mV/cm,y轴分度值10

V/cm)

有时在无微波辐照的条件下，我们无法观测到约瑟夫森临界电流，但是在施加小功率微波辐射的条件下，能观测到电压不为0，也足以证明直流约瑟夫森效应的存在。因为我们在小功率的微波辐照下，仍然观测到的超导微桥的伏安特性曲线没有电压不为0的现象。这说明此处的电压不为0是达到约瑟夫森临界电流所导致的，而不是因为达到超导临界电流。

在微波辐照下，我们绘制出了高温超导双晶约瑟夫森结的V−I曲线如下：

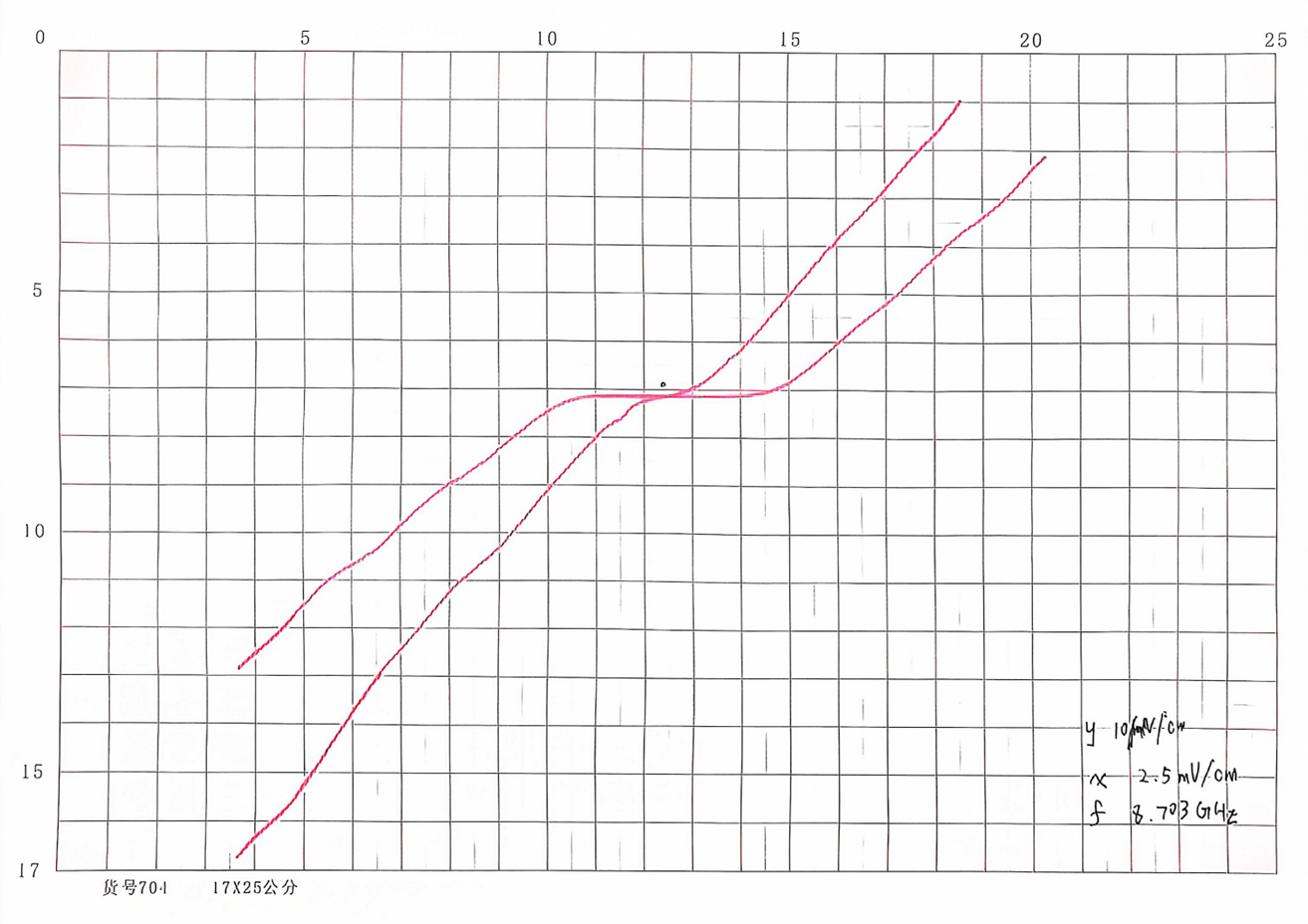
图10：微波辐照下，高温超导双晶约瑟夫森结的电压-电流变化曲线(x轴分度值2.5mV/cm,y轴分度值10μV/cm)

如图，可以看到较为明显的微波感应台阶。没有特别明显的原因是材料存在久用的问题。我们选择台阶更为明显的曲线进行spline操作，测量得到各台阶高度数据如表1所示：

	-2	-1	0	1	2
	-3.55	1.80	0	1.75	3.55
	-35.5	-18.0	0	17.5	35.5

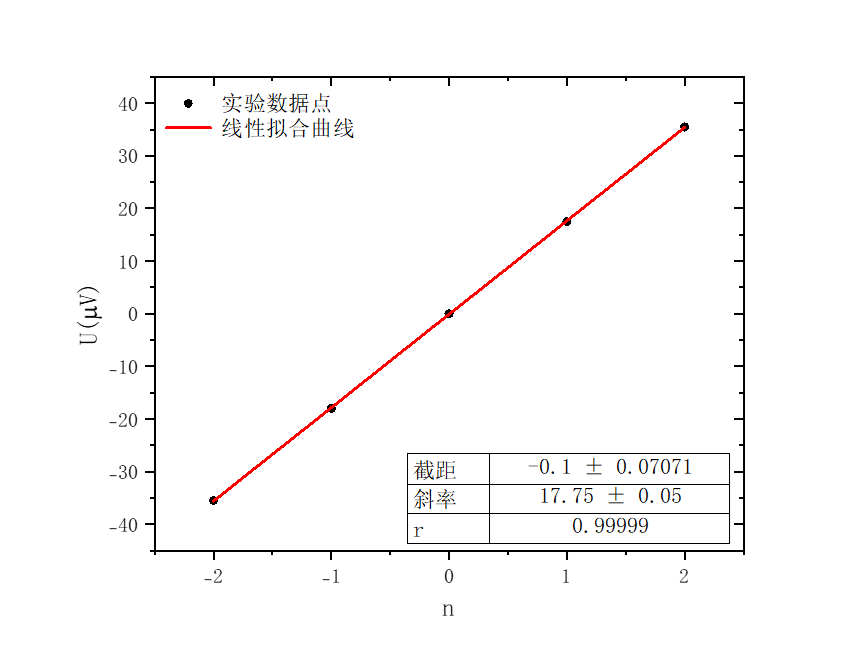
线性拟合得到结果如图11所示：

图11：微波台阶高度与微波台阶序数线性拟合结果

拟合直线斜率为。利用公式，计算得微波频率理论值为。而微波频率标称值为，理论值与标称值基本一致。该现象验证了交流约瑟夫森效应的存在。同时，理论预测值与实际标称值的基本温和，也证明约瑟夫森效应理论预测的正确性。

差异可能来源于:

坐标纸上曲线太粗，读坐标值存在误差。
样品收到的微波信号不是完美正弦波，导致理论存在偏差。
微波发生器标称值存在误差，或X-Y记录仪绘图存在误差。

结论

本次实验中，我们使用高温超导体YBa₂Cu₃O_7−x 令两块材料在平行于衬底表面方向的晶向不同，并将其粘接在一起，构成双晶约瑟夫森结。实验中我们对比了该双晶约瑟夫森结与同尺寸同材料的超导微桥的电阻-温度曲线，发现二者的超导转变温度基本一致，这表明了二者在电阻-温度依赖方面的相似性。我们在小功率微波辐照或无辐射的条件下，对比了双晶结与超导微桥的伏安特性曲线，前者会出现约瑟夫森临界电流，从而出现电压不为0的区域，而后者则一直保持电压为0，这表明约瑟夫森结中的弱连接的确会改变超导材料的性质，同时证明了直流约瑟夫森效应的存在。我们又在一定功率、频率的微波辐照条件下，观测到了明显的微波感应台阶现象，证明了交流约瑟夫森效应的存在。同时，利用台阶高度计算微波频率理论预测值，与实际标称值基本吻合，这进一步证明了约瑟夫森效应理论预测的正确性。

参考文献

[1] ONNESK. Theresistance of pure mercury at helium temperatures[J]. Commun. Phys. Lab. Univ. Leiden, b, 1911, 120.

[2] LONDON F, LONDON H. The electromagnetic equations of the supraconductor[J]. Proceedings of the Royal Society of London. Series A Mathematical and Physical Sciences, 1935, 149(866): 71-88.

[3] BARDEENJ, COOPERLN,SCHRIEFFERJR. Theory of superconductivity[J]. Physical review, 1957, 108(5): 1175.

[4] BEDNORZJG,MÜLLERKA. Possible high t c superconductivity in the ba- la- cu- o system[J]. Zeitschrift für Physik B Condensed Matter, 1986, 64(2): 189-193.

Supplement：思考题

在进行R−T曲线测量时如何选定坐标记录原点和X−Y 记录仪的分度值以得到合适的测量曲线？

坐标原点选定在坐标纸左下角，且最好在格点上。将x轴和y轴均置于“measure”模式，调节x轴和y轴的分度值，使得笔尖位置位于坐标纸右上角。这样得到的R−T曲线能尽可能铺满坐标纸。
通过测量V−I曲线来考察直流约瑟夫森效应时，X−Y记录仪轴(结电压)的分度值在开始时应该选定在什么挡位？是应该大还是应该小？

y轴分度值应尽可能小，这样才方便辨别曲线何时开始弯曲，即电流何时到达约瑟夫森临界电流。但分度值也不能取到最小，因为这样噪声过大，可能影响判断。
随着微波输出功率的变化，双晶约瑟夫森结的伏安特性(V−I)曲线有什么变化？产生的原因是什么？

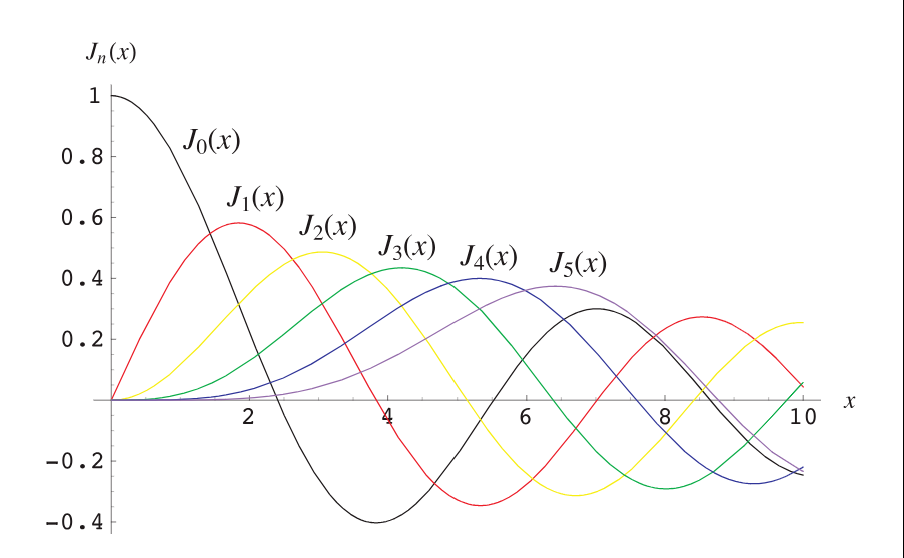
图12：Bessel函数图像

根据式(9)，在微波台阶处，直流分量大小正比于，这表明各台阶长度变化与贝塞尔函数行为相同。当微波功率增大时，u变大，即贝塞尔函数宗量增大。对于，0级台阶先变短后变长；对于，1级台阶先变长后变短……各级台阶长度变化行为与图示的各阶贝塞尔函数变化行为相同。

双晶结超导微桥与不含有双晶结的超导微桥的测量结果有什么差异？这些差异为什么可从一个侧面证实约瑟夫森效应的观测？

无微波辐照时，当大于约瑟夫森临界电流时，双晶结超导微桥上电压不再为0；有微波辐照时，双晶结超导微桥伏安特性曲线出现微波感应台阶。而不含有双晶结的超导微桥的电压在实验测量电流范围内均为0。这种差异意味着双晶结确实导致样品的超导性质改变，即形成了弱连接，而同样尺寸的微桥结构则不会改变样品的超导性质。同时，双晶结电压大于0时对应的临界电流明显小于超导微桥的临界电流，这说明二者的机制是不同的。实际上，前者是约瑟夫森临界电流，达到临界电流后会发生单电子隧穿，导致电压升高；而后者是超导临界电流，达到临界电流后，材料发生相变，失去超导性质。同时，微波感应台阶的观测也证明了交流约瑟夫森效应是存在的，进一步验证约瑟夫森效应的预测。
为什么说超导是宏观量子现象？通过此实验, 谈谈你对这个问题的理解。

通常的量子效应都是微观尺度的，即粒子尺度，例如汤普孙散射、斯特恩-盖拉赫实验，其量子现象的尺度都是粒子或粒子束。而超导以及约瑟夫森效应的现象是宏观的电流、电压，这个尺度的量是容易观测的。同时，超导是因为大量库伯对相干凝聚到同一量子态，导致库伯对可以无散射的移动，而约瑟夫森效应是因为库伯对的量子隧穿，这些都是量子效应，但是在宏观尺度就可以观测，故称为宏观量子效应。
约瑟夫森效应有哪些应用(你了解或设想的), 这些应用的基本原理是什么？

约瑟夫森效应在量子线路领域有重要应用，包括超导量子干涉仪、超导量子比特等。超导量子干涉仪是一种极高灵敏度的磁力计。其结构包括一个由两个约瑟夫森结构成的超导线圈。没有外场时，输入电流分为两路；有外场时，会产生感生电流，与原来两路电流方向一个同向一个反向流入，当任何一路电流超过约瑟夫森临界电流时，结两端产生电压，从而探测到微小磁场。约瑟夫森效应还用于精确标定电压单位。因为约瑟夫森效应提供了电压和频率之间精确的对应关系，而频率可以通过铯原子钟精确测量，因此利用约瑟夫森效应可以精确确定电压。