摘要： 远离平衡态的开放系统会出现分岔行为，系统将离开原来的无序热力学分支，发生突变进入稳定有序状态，这种有序结构被称为“耗散结构”。耗散结构理论可以解释自然科学和人文社会科学的诸多领域的问题，是少数能横跨多学科的重要科学理论之一。对于自由面-固壁底层的流体薄层的热对流系统，即瑞利-贝纳德热对流系统，远离平衡态时会出现非线性热对流斑图。本文章的实验旨在观察改变盛满水的容器上下表面温度差时，不同厚度的水层内部的热对流斑图发生涌现的过程，来对开放系统和耗散结构做出初步的了解。实验中采用阴影法，通过CCD接收图像的敏感分布，反映水层内不同位置的密度差异，并粗略判断2mm和4mm厚度的水层对称性发生破缺，也就是出现斑图的临界温度。

关键词：热对流、耗散结构论、对称性破缺、阴影法

引言

自从热力学理论建立之初，一直困扰人们的问题之一就是自组织现象发生的原理和过程。小到化学反应的周期振荡^[1-3]，大到生命的起源和存续，这种看似不符合热力学第二定律的自然现象反映了自发对称性破缺^[4-5]这一重要的物理原理。

20世纪60年代，以普利高津为首的比利时布鲁塞尔学派提出耗散结构理论^[6-7]。该理论描述一个远离平衡的开放系统，当系统离开平衡态的参量达到一定阈值，系统会出现分岔行为，从无序状态突变到一个全新的稳定有序状态，这种有序结构称为耗散结构。耗散结构理论不仅能解释许多物理、化学、生物等自然科学文体，近年来还被引入哲学、社会学、经济学等诸多领域，使之称为少数能横跨自然与人文社会科学的重要科学理论之一。

1900年，贝纳德对具有自由面-固壁底层的流体薄层进行了热对流实验^[8-9]，观测到了各种对流图形，后来瑞利对该系统进行了理论分析。因此，该系统被称为瑞利-贝纳德热对流系统。该系统由瑞利数描述，当瑞利数超过阈值时，系统由稳定状态演化到不稳定状态。

流体系统的热对流行为伴随着流体的温度变化，导致流体密度、折射率产生不均匀分布。利用阴影法，使激光照射在流体上，观察不均匀折射率分布导致的反射光强不均匀分布，产生热对流斑图，从而实现流场温度分布可视化。

本实验通过观察2mm，4mm对流水层的非线性热对流斑图随温差增加的状态演化，分析耗散结构基本特征，加深对于耗散结构理论的理解。20世纪60年代，以普利高津为首的比利时布鲁塞尔学派提出耗散结构理论\cite{intro6,intro7}。该理论描述一个远离平衡的开放系统，当系统离开平衡态的参量达到一定阈值，系统会出现分岔行为，从无序状态突变到一个全新的稳定有序状态，这种有序结构称为耗散结构。耗散结构理论不仅能解释许多物理、化学、生物等自然科学文体，近年来还被引入哲学、社会学、经济学等诸多领域，使之称为少数能横跨自然与人文社会科学的重要科学理论之一。

1900年，贝纳德对具有自由面-固壁底层的流体薄层进行了热对流实验\cite{intro8,intro9}，观测到了各种对流图形，后来瑞利对该系统进行了理论分析。因此，该系统被称为瑞利-贝纳德热对流系统。该系统由瑞利数描述，当瑞利数超过阈值时，系统由稳定状态演化到不稳定状态。

本实验通过观察2mm，4mm对流水层的非线性热对流斑图随温差增加的状态演化，分析耗散结构基本特征，加深对于耗散结构理论的理解。

原理和理论

本实验的对流系统如图1所示^[10], 温度分别维持为和。

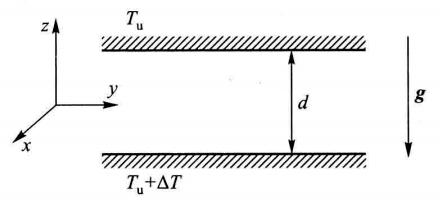
图1：上下温度不同的两无限大平板间的热对流系统

此热对流系统满足Boussinesq条件，相应的热对流基本方程组为：

$\begin{cases} \frac{\partial V}{\partial t}+\mathbf{V}\cdot\nabla V=g\alpha Tz-\frac{1}{\overline{\rho}}\nabla p+\gamma\nabla^2\mathbf{V}\\ \nabla\cdot\mathbf{V}=0\\ \frac{\partial T}{\partial t}+\mathbf{V}\cdot\nabla T=\kappa\nabla^2 T \end{cases}$

其中，为流体速度场，分别为流体的热膨胀系数、黏度和热导率，为流体的平均密度。结合以下三个边界条件：

$\begin{cases} T(z=-d/2)=T+\Delta T\\ T(z=d/2)=T\\ V=0,~~z=\pm d/2 \end{cases}$

上述方程有定常解：

$T_0(z)=T_u+\Delta T(1/2-z/d),~~V_0=0$

回代入方程(1)中，得到关系：

$g\alpha T_0(z)\hat{z}-\frac{1}{\overline{\rho}}\nabla p_0(z)=0$

利用线性稳定性分析方法分析定态解的稳定性。假设存在微扰，代入方程(1)中，去量钢化，可以得到微扰满足的方程：

$\begin{cases} \sigma^{-1}\left(\frac{\partial u}{\partial t}+\mathbf{u}\cdot\nabla\mathbf{u}\right)=\theta\hat{z}-\nabla p+\nabla^2\mathbf{u}\\ \nabla\cdot\mathbf{u}=0\\ \frac{\partial \theta}{\partial t}+\mathbf{u}\cdot\nabla\theta=R\alpha\omega+\nabla^2\theta \end{cases}$

其中，边界条件为被称为瑞利数，是微扰速度在方向上的分量。

采用线性近似，将方程中欧给的非线性项忽略掉，并假设初始微扰为，其中，为复数。数值计算结果表明，存在一个临界参量：

$R_c=1707.76,~~~~~~~~q_c=3.117$

当对流水层的温度差使得瑞利数$RaR_c $时，满足条件的噪声随时间增大，如方程中给出的$ q_c $，当其大到一定程度时，非线性项就不再可以忽略了，可以采用多尺度分析理解斑图的分岔行为。最后，当$ Ra $显著大于$ R_c$时，有规律的对流斑图不足以提供上下面间的热流，系统对流失稳，转变为湍流。

实验装置

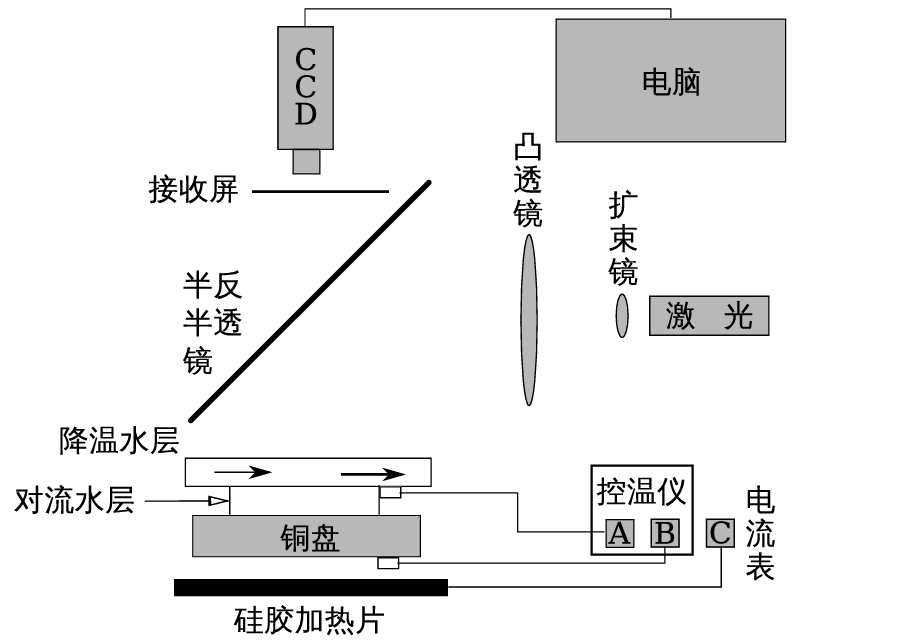
图2：实验装置示意图

实验装置如图2所示：受观察的液层通过橡胶垫圈来控制厚度为，或，上下界面分别选用透明的蓝宝石片和反射率高的铜。此二者的热导率都很高，用来保持恒温。实验中通过改变通过预置在铜盘下方的电热丝的电流，从而改变下界面的预设温度。抽水泵连续而稳定地使降温水层循环流动，保持上界面的温度不变，从而在上下两界面间创造稳定的温度差。
实验通过阴影法观察对流斑图，以准平行光正入射液层，考察经底面铜盘反射的光强分布，间接反映水层内的折射率差异。根据费马原理，垂直于光传播方向上若有折射率的梯度差异，则会使光向着高折射率的方向偏转，因此接收屏上的亮区即对应高折射率的水域，也就是高密度的冷水沉降区域。通过观察CCD接收到图像的明暗条纹，就可以判断水层中的对流结构。具体的实验步骤请参考Supplement B中所描述的方法。

实验结果与分析

2mm对流水层斑图

未通入电流时，上下表面温度分别为 $上$ ， $下$ 。差异是因为接触电阻不同。实验测得通过硅胶片电流和对应水层上下表面温度差数据详见Supplement C中的表1。实验测得的不同温差下，2mm对流水层的热对流斑图如图3所示。

图3：2mm对流水层在不同温差下的热对流斑图

时，图像亮度均匀，未出现斑图，即系统仍处于无序状态。
时，图像中开始出现对比度极低的同心圆(事实上上面的半圆还没有能被肉眼辨别出来)，出现斑图，此时系统突变为有序结构。由于系统具有圆形的边界条件，可以预见，斑图应具有一定对称性。2mm水层出现斑图的临界温差大约为。
随着温差增大，斑图条纹变得细锐，对比度变高。这是是因为随着温差变大，下表面向上传递的热量变多，导致向上运动的热水变多，温度变高，热水对应暗条纹，因此，暗条纹变粗变暗，条纹变得细锐，对比度变高。
时，图像左上边缘出现鳞片状条纹。这可能是因为随着温度升高，水层侧面散热无法忽略，同时降温水层不能保证上表面温度均匀，边界条件被破坏，因此出现了更复杂的条纹形状。随着温差升高，边缘的鳞片状条纹变大变多。
时，图像中心条纹由亮条纹变为暗条纹。这是因为随着温差升高，条纹尺寸变大，使得图像中心出现了条纹吞吐。

4mm对流水层斑图

水层厚度加倍，瑞利数随着温差的变化更剧烈，这使得我们可以观察系统更加远离平衡态时的行为。实验测得通过硅胶片电流和对应水层上下表面温度差详见Supplement C中表2中提供的数据。实验得到的不同温差下，4mm对流水层的热对流斑图如图所示。

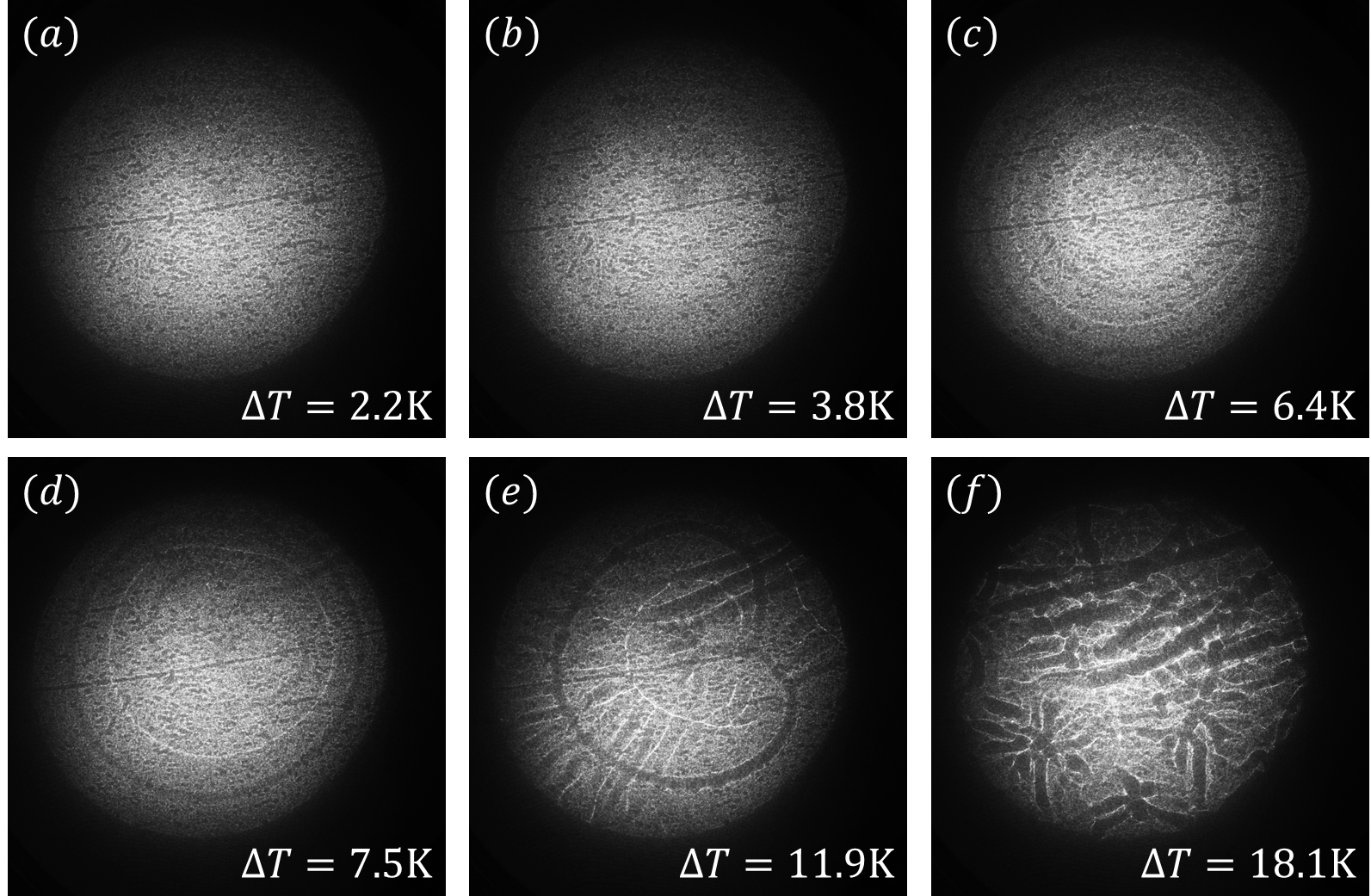
图4：4mm对流水层在不同温差下的热对流斑图

温差较小时，图像亮度均匀，未出现斑图；直到时，出现了隐约可见的圆形条纹，我们估计此温度为临界温度。如果没有出现预期的同心圆条纹一部分是因为制备水层后静置时间不够，导致初始时，水层并非静止。当温差达到6.4K时，就已经出现了亮暗极为分明的同心圆条纹；知道温差到达7.5K时，圆对称性逐渐被打破，内圈亮条纹出现吐出的现象，使斑图中心逐渐变暗。
当温差到达之后，各个圈层的形状均开始出现畸变，呈现出爱心形条纹，并且每一层之间都有很多细密的条纹相互连接，可以看出体系的对称性正在被打破，但是体系仍然存在一些自发的对称性。
时，斑图变得更加复杂，系统出现分岔行为，条纹呈现树杈状的分形结构。这是因为此时温差过大，系统偏离平衡态过多，分形状的对流行为可以提高热对流效率，实现更多的热量传递。温度继续升高时，系统完全丧失稳定结构，形成复杂的湍流。

斑图出现的共同特征和阶段

观察斑图出现，即由稳定态转变到对流态的过程，无论是2mm水层还是4mm水层，他们都有一些共同的特征，我们下面就根据实验结果定性的给出斑图演化的一些特点。

斑图涌现

当温度差达到一定阈值时，对流结构自发地从无到有地出现，建立起稳定的对流结构。2mm水层的实验中，这种突变发生在两张图之间，而这说明对称性破缺的发生是临界点附近的突变行为，而非逐渐过渡的过程(这是上课说的结论，但就我这个实验结果来看我还真有点质疑这个论断QWQ，我感觉这图3(b)真就像是一点点出现的斑图，也有可能最开始出现的斑图就是肉眼不可见的，但是确实是突变产生的，后续一直在增强)。

对称结构

可以看出对流斑图基本呈现出同心圆的结构。这种结构的生成和实验中选取的圆形的边界条件紧密相关。如果选择如理论计算中采用的无穷大的边界，则系统不会自发生成同心圆这种中心对称的结构，而是六角形斑图等具有平移对称性的结构。

初值依赖

如果初始没有静置30分钟，可能会看到水层没有呈现出中心对称的同心圆结构，而是非同心圆或椭圆甚至更加紊乱。这种现象的发生与发生对称性破缺时系统的初条件（水层内部的微小运动速度，不均匀的温度场等）有关。由于在以上，系统的小微扰会被指数放大直到线性近似不再成立，因此初始微扰的取值将直接影响系统最终平衡时的对流结构。这种微扰放大和初始条件强烈依赖的混沌性质，也正是复杂系统最显著的特点之一。

定常流动

当经历足够长的时间后，无论斑图空间结构多么复杂，对流都将不再随时间变化，系统做定常流动。这说明，作为耗散结构的复杂系统有保持自身结构和远离平衡态的能力，非线性方程组在其解附近的扰动具有指数衰减的性质。

衬比度

随着温差增加，对流斑图的明暗差异对比度增强，即亮纹更亮，暗纹更暗，而形态基本保持不变。明暗差异的增大意味着水层中密度差异增大，传热和对流都加快，这是增大热流量后的正常现象。

空间结构和边条件

在实验中明显观察到，4mm相比2mm的亮纹间距更大，也更易形成对称的圆环结构。理论计算表明，当对流斑图开始发生时，斑图驻波的特征空间尺度为，其中由数值计算得到。这也就是说，斑图（也即速度场）的半波长与水层的厚度相当，当水层厚度变为倍时，波长也变为倍。水盘的半径和水盘的厚度之比决定了水层受环形边界条件影响的强度。越大，越大，系统越接近于无穷大平行平板，受环形的中心对称边界的影响越小，越不易形成同心圆斑图（一个显然的观察是，在无穷大平行平板间，任何点都具有平等的地位，以某一点为圆形形成大量同心圆的可能性为零）。而越小，侧面边界上的边界条件造成的影响就越显著，系统就越容易形成同心圆。

水层厚度对临界温差的影响与误差分析

在理论推导中，由和临界条件可知增大水层厚度时临界温差将立方反比地减小。而实际情况下测得，2mm水层的突变发生在，4mm水层的突变发生在，实验测得的结果并不完全支持立方反比的结论。这种现象的发生有几何和散热两方面的原因。几何上，上述的计算是基于无穷大平行平板得出的，与实际的有限环形区域有差异。散热上，的计算中认为侧壁是完全绝热的，而实际中橡胶垫圈的散热不可忽略。这两方面的差异共同导致了实验结果与理论的不同。

结论

本实验观察了2mm，4mm对流水层的斑图随上下表面温差的变化行为。总的来说，随着温差升高，系统由无序突变到有序，当系统进一步远离平衡态时，系统出现失稳，出现分岔结构，最终演化为湍流。
在2mm水层中，我们观察到随着温差增大，斑图尺寸增加，衬比度增加。其临界温度差约为。
在4mm水层中，我们观察到随着温差增大，系统逐渐偏离平衡态，斑图分裂，出现分岔结构，最终演化为湍流。其临界温度差。
通过本实验，认识并检验了耗散结构的基本特征，初步了解了非线性物理的分析手段。

参考文献

[1] HOLLÓJ,SZEJTLI J. The mechanism of starch-iodine reaction[J]. Periodica Polytechnica Chemical Engineering, 1958, 2(1): 25-37.

[2] SULLIVANJH. Mechanism of the“bimolecular”hydrogen—iodine reaction[J]. The Journal of Chemical Physics, 1967, 46(1): 73-78.

[3] MARTÍNEZC,MUNIZK. Aniodine-catalyzed hofmann–löffler reaction[J]. Angewandte Chemie International Edition, 2015, 54(28): 8287-8291.

[4] BEEKMANA, RADEMAKERL, VAN WEZEL J. An introduction to spontaneous symmetry breaking[J]. SciPost Physics Lecture Notes, 2019: 011.

[5] SUSSKINDL. Dynamics of spontaneous symmetry breaking in the weinberg-salam theory[J]. Physical Review D, 1979, 20(10): 2619.

[6] PRIGOGINEI, NICOLIS G. Self-organization[J]. Non-equilibrium system, 1977, 28.

[7] PRIGOGINEI,LEFEVERR.Symmetry breaking instabilities indissipative systems.ii[J]. The Journal of Chemical Physics, 1968, 48(4): 1695-1700.

[8] BODENSCHATZE,PESCHW,AHLERSG. Recent developments in rayleigh-bénard convection[J]. Annual review of fluid mechanics, 2000, 32 (1): 709-778.

[9] ROCHEPE,CASTAINGB,CHABAUDB,etal. Sidewalleffectsinrayleighbénardexperiments[J]. The European Physical Journal B-Condensed Matter and Complex Systems, 2001, 24: 405-408.

[10] 周路群,冉书能,贾春燕. 非线性热对流斑图实验[J]. 物理实验,2012(8): 1-5.

Supplement A：思考题

随着温差的升高，可以看到黑白结构的出现，黑白的区域如何对应水层的流动情况?

根据费马原理，垂直于光传播方向上若有折射率的梯度差异，则会使光向着高折射率的方向偏转，因此接收屏上的亮区即对应高折射率的水域，也就是高密度的冷水沉降区域。反之，接收屏上的暗区即对应低折射率的水域，也就是低密度的热水上浮区域。
斑图出现的临界点如何确定?如何根据所观察的现象确定临界点?

首先实验前，根据经验参数选取合适的电流大小取值，以保证覆盖系统的临界温度所处的位置。实验中，当温差从小的方向接近预期临界值时，要减小电流间隔，每次系统充分稳定后拍照。照片全部拍摄完毕后，根据亮暗纹完全清晰稳定后的较高温差斑图不断在较低温差图中对照，寻找能模糊看到这些亮暗纹的温差最低的一张图片，作为临界温度。注意，对照中要忽略干涉条纹和摩尔纹的影响。
当水层换成4mm时，考虑临界点会如何改变?

理论推导认为，水层厚度翻倍，临界温差将减小为。而实际情况下测得，2mm水层的突变发生在，4mm水层的突变发生在，并不完全支持立方反比的结论。这种现象的发生有几何和散热两方面的原因。几何上，上述的计算是基于无穷大平行平板得出的，与实际的有限环形区域有差异。散热上，的计算中认为侧壁是完全绝热的，而实际中橡胶垫圈的散热不可忽略。
如何确定斑图的空间特征尺度?

斑图中条纹的亮暗反映了水层各个位置的密度差异，两条亮纹之间的距离就近似等于密度分布的空间周期，也就是。由上文的计算，故两条亮纹之间的距离近似等于液层的厚度，也就反映了斑图的空间特征尺度。
斑图的空间特征尺度与对流水层厚度的关系如何?

正如在上一问题中提到的，斑图的空间特征尺度，也就是波长λ，近似等于水层厚度的两倍。

Supplement B：实验步骤

调整光路，使接收屏上出现亮度均匀的圆形红色图案，并利用软件观察
接通水阀，确定降温水层流动正常
加入厚度2mm的黑色O环，等待40min，使水层静止
开启温控仪，此时温控仪示数为室温
改变硅胶片加热电流，从而改变温度差，等待10min，使水层内热对流稳定，观察并记录温度差的相对应的稳定斑图
重置4mm O环额厚度水层，观察斑图随温差增加的状态演化。

Supplement C：实验数据

除了实验中通过高速摄像机拍摄的斑图形状之外，我们还会测量上下表面温度差对于输入电流的依赖关系，两次测量的数据如表1和表2所示。

序号	电流()	$上$	$下$
1	0.607	26.2	30.9	4.7	3.8
2	0.798	28.0	35.6	7.6	6.7
3	0.854	29.2	38.0	8.8	7.9
4	0.900	30.4	40.0	9.6	8.7
5	0.948	31.6	41.8	10.2	9.3
6	1.006	32.7	43.6	10.9	10.0
7	1.097	34.5	46.6	12.1	11.2
8	1.196	36.5	49.9	13.4	12.5
9	1.307	38.8	54.0	15.2	14.3

表1：2mm水层测量数据表(表格中ΔT'为扣除零点温差后的修正值)

序号	电流()	$上$	$下$
1	0.192	29.7	30.5	0.8	0
2	0.396	29.6	31.8	1.2	0.4
3	0.613	30.1	33.9	3.8	3.0
4	0.901	32.6	40.1	7.5	6.7
5	1.194	36.2	48.1	11.9	11.1
6	1.488	41.9	60.0	18.1	17.3

表2：4mm水层测量数据表(表格中ΔT'为扣除零点温差后的修正值)