摘要： 当铁磁材料处于外磁场时，特定频率的电磁波被材料共振吸收的现象称为铁磁共振(FMR)。铁磁共振具有磁共振的一般特性，被广泛应用于光谱技术、高频电子设备等领域。本实验使用反射式速调管作为微波信号源，观测了速调管的振荡模和传输式谐振腔的谐振曲线，得到了谐振腔的有载品质因数。在传输式谐振腔中，逐点测绘多晶铁氧体样品对微波的吸收曲线，观测到了铁磁共振效应。通过测量共振磁场和共振线宽，计算出了样品的g因子和弛豫时间。

关键词：铁磁共振，传输式谐振腔

引言

谐振腔是常用的微波元件之一^[1]，在微波技术中一般用作谐振腔波长计^[2]、微波电子管^[3-4]的组成部分或测量腔等。微波磁共振是微波与物质相互作用所发生的物理现象，磁共振方法已被广泛用来研究物质的特性、结构和弛豫过程。铁磁共振具有磁共振的一般特性，而且效应显著，用简单装置就可以进行观测。

铁磁共振现象在1911年被首次观测。1935年，物理学家朗道和利夫希兹预测了拉莫尔进动会导致铁磁共振效应。这种效应广泛应用于光谱技术和高频电子设备领域。FMR光谱技术用于探测铁磁材料的磁化强度，是探测自旋波和自旋动力学的标准工具。

本实验使用反射式速调管^[5]作为微波信号源，在传输式谐振腔中，观测多晶铁氧体样品的铁磁共振效应。实验旨在通过观测铁磁共振和测定有关物理量，掌握微波信号源的使用方法和谐振腔的工作特性，了解用谐振腔法观测铁磁共振的测量原理和实验条件，加深磁共振的一般特性的理解。

理论

传输式谐振腔

谐振条件

一个封闭的金属导体空腔可以用来做微波谐振腔。由一段标准矩形波导管，在其两端加上带有耦合孔的金属板，就构成一个传输式谐振腔。谐振腔发生谐振时，腔内电磁波为驻波，腔长与波导波长满足：

$l=p\cdot\frac{\lambda_g}{2}$

其中，，。

品质因数与谐振曲线

品质因数(Q值)是用于表明谐振腔效率高低的量。品质因数的一般定义为：

$Q=\omega_0\frac{\text{谐振腔内总储能}}{\text{每秒耗能}}=\omega_0\frac{W_{\text{储}}}{W_{\text{耗}}}$

如图1，微波线路中，微波信号源输出的功率经过隔离器进入谐振腔，然后为检波器所接收。

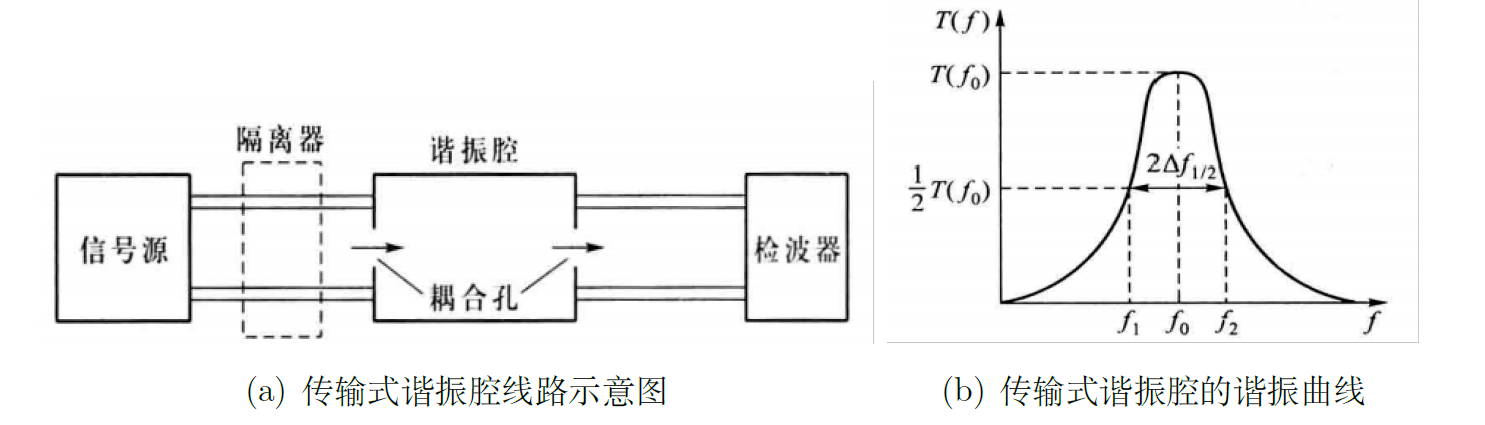
图1：传输式谐振腔的品质因数与谐振曲线

图1：传输式谐振腔的品质因数与谐振曲线^[6]

传输式谐振腔的传输系数T(f)定义为：

$T(f)=\frac{P_{\text{出}}(f)}{P_{\text{入}}(f)}$

Q值足够高时，有：

$T(f)=\frac{T(f_0)}{1+4Q_L^2\left(\frac{\delta f}{f_0}\right)^2}$

其中，，。如图1，传输系数的曲线即为谐振曲线。对于半功率点，有：

$Q_L=\frac{f_0}{2\Delta f_{1/2}}$

在微波测量中，先测量谐振腔谐振时的微波频率(此时输出功率最大)，然后测量输出功率降至一半时的微波频率和，则有载品质因数为：

$Q_L=\frac{f_0}{|f_1-f_2|}$

反射式速调管的工作特性

如图2，反射式速调管主要由阴极、谐振腔和反射极三部分组成。从阴极飞出的电子被谐振腔上的正电压加速，穿过栅网，在反射极反向电压的作用下，电子返回栅网，从而产生微波振荡。

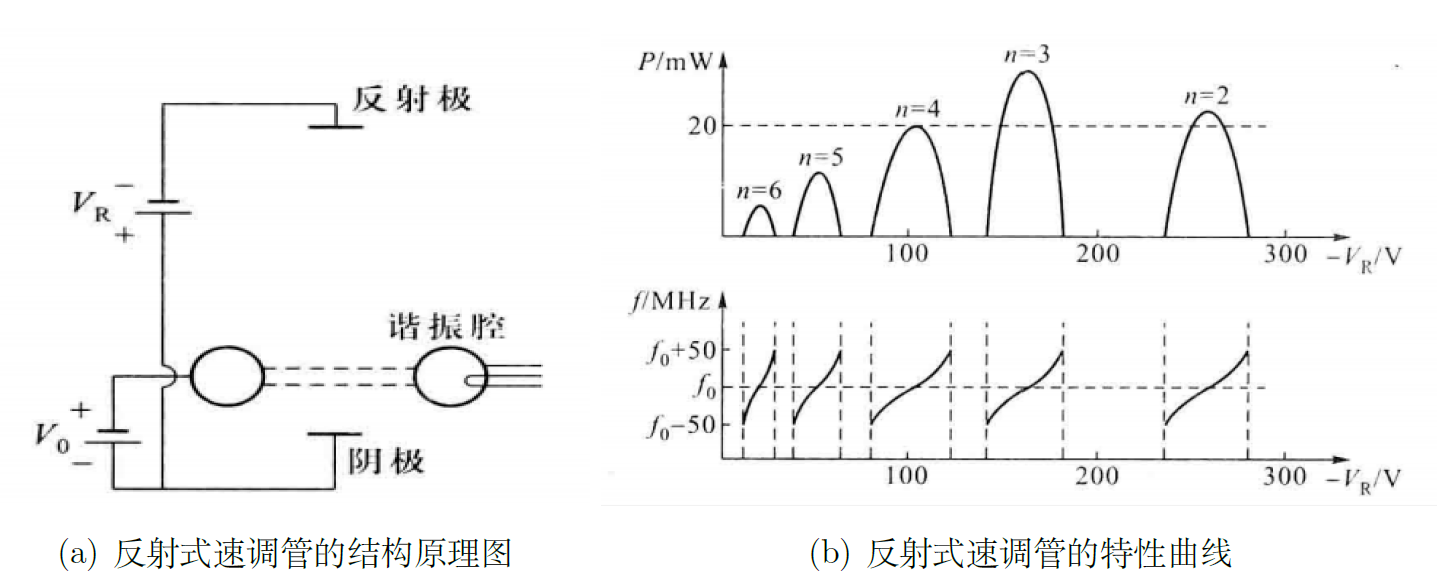
图2：传输式谐振腔的品质因数与谐振曲线

图2：传输式谐振腔的品质因数与谐振曲线^[6]

反射式速调管的特性曲线如图2所示。可以看出以下特性：具有分立的振荡模、改变反射极电压会引起微波功率和频率的变化、存在最佳振荡模、各个振荡模的中心频率相同。

反射式速调管的振荡频率可以通过“电子调谐”(改变反射极电压)来小范围调节，或通过“机械调谐”(调节调谐螺钉，改变谐振腔大小)来较大范围调节。

铁磁共振

处于微波磁场和恒定磁场中的微波铁氧体，微波磁感应强度可表示成：

$\mathbf{b}=\mu_0\overset{\leftrightarrow}{\mu}\cdot\mathbf{h}$

其中，

$\overset{\leftrightarrow}{\mu}= \begin{bmatrix} \mu&-i\kappa&0\\ i\kappa&\mu&0\\ 0&0&\mu_z \end{bmatrix}$

均为复数，为实数，即。

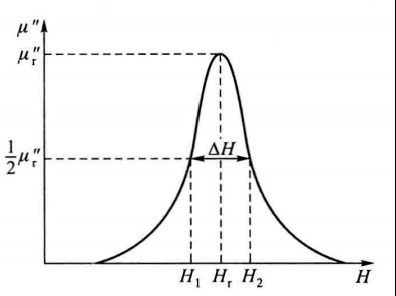
图3：铁磁共振曲线

图3：铁磁共振曲线^[6]

微波铁氧体处在频率为的微波磁场中，改变恒磁场时，将发生铁磁共振现象。此时曲线上出现共振峰，峰值对应磁场称为共振磁场，两点对应磁场间隔称为铁磁共振线宽，表征磁损耗大小。

多晶体样品发生铁磁共振时，满足：

$\omega_r=\gamma H_r$

其中，。当磁场改变时，趋于平衡态的过程称为弛豫过程，弛豫所需的特征时间称为弛豫时间，有：

$\tau=\frac{2}{\gamma\Delta H}$

测量铁磁共振线宽的实验方法

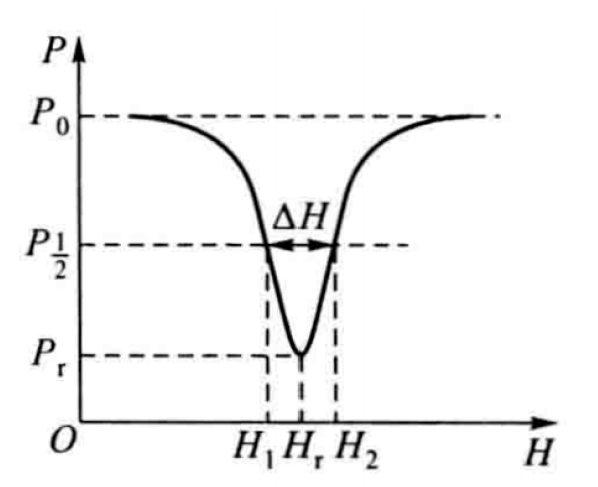
图4：输出功率P与磁场H的曲线

图4：输出功率P与磁场H的曲线^[6]

实验过程中，需要满足下列实验条件：

球很小，可看成一个微扰，放在腔内微波磁场最大、微波电场为零处
谐振腔始终保持在谐振状态
微波输入功率保持恒定不变

如果在测量过程中不逐点调谐，而样品的频散效应又不能忽略，可以理论上进行修正。修正后，半功率点对应功率为：

$P_{1/2}=\frac{2P_0P_r}{P_0+P_r}$

在实验中，我们在远离铁磁共振区域保证微波频率与谐振腔谐振，测量曲线时不逐点调谐，而利用式(11)计算出，再从曲线上定出。

实验

实验装置

本实验的装置如图5所示。该装置可以在3cm波段观测。

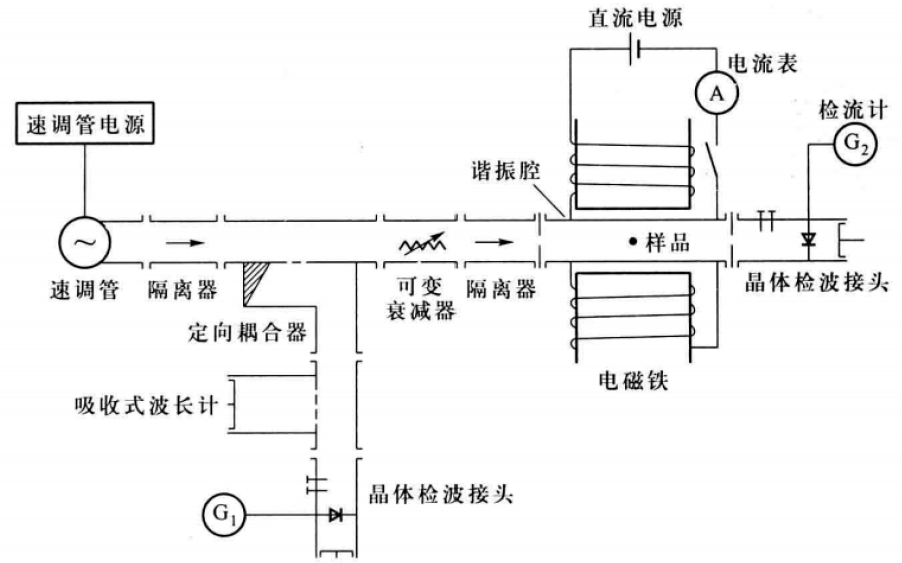
图5：实验线路

图5：实验线路^[6]

实验中，速调管到第二个隔离器这部分集成在XFL-2A厘米波信号发生器中。其中，速调管用于产生微波信号，吸收式波长计和微安表G1用于测量微波波长，可变衰减器用于调控输入谐振腔的微波功率。

传输式谐振腔采用型矩形谐振腔。样品为多晶铁氧体小球。

晶体检波接头满足平方律检波，其检波电流表示相对功率()。检流计G2使用AC15/4 直流复射式检流计，用于观测传输式谐振腔的输出功率。

电磁铁用于提供恒定磁场，其中直流电源使用WYJ-9B型晶体管稳压电源，电流表使用PA15A型直流数字电流表。

实验步骤

观测速调管的振荡模，测量一个振荡模的中心频率和电子调谐范围

打开信号发生器，预热10分钟，将“断-连续-调制”旋钮置于“连续”位置，衰减旋钮置于衰减量最小处。
调节反射极旋钮，观察速调管的振荡模。调节检波电流旋钮，使电流最大读数在量程3/4处，此后保持检波电流不变。记录最大电流I。
调节波长表旋钮，使电流减到最小，此时波长对应中心频率。
调节波长表旋钮使之失谐。分别朝两个方向调节反射极旋钮，使电流为最大电流的一半。分别测量其对应频率，，得到电子调谐范围。

观察传输式腔的谐振曲线，测量腔的有载品质因数

打开检流计。在信号发生器的电流最大位置的附近慢慢调节反射极旋钮，观察谐振曲线。
调节反射极旋钮，使检流计示数最大，此时达到谐振状态。调节可变衰减器，使最大电流不超过检流计量程，测量此时的频率和检流计格数P。
分别朝两个方向调节反射极旋钮，使检流计格数为最大值的一半。分别测量对应频率，，计算出有载品质因数。

用简便方法测量共振磁场和线宽

将变阻器阻值调到最大，打开直流电源，并对谐振腔调谐。
改变变阻器阻值，记录检流计最大读数，最小读数，中点读数，以及对应的电流表读数。
反复测量3次，每次都重新进行调谐。
查表得到磁场H的值，确定共振磁场和线宽。

逐点测绘P−H曲线

将变阻器阻值调至略大于检流计读数开始有变化的位置，并进行调谐。
改变变阻器的阻值，逐点记录检流计读数及对应的电流表读数。查表得到，绘制曲线。(注意由于磁滞效应，变阻器阻值只能向一个方向变动)

实验结果和讨论

观测速调管的振荡模，测量一个振荡模的中心频率和电子调谐范围

调节反射极旋钮，电流呈“不变-增大-减小-不变-增大”的变化趋势，从开始增大到结束减小即对应速调管的一个振荡模。

波长计波长-频率关系为。测量结果如表1所示：


52	3.827	9206.26
26	3.833	9204.99
26	3.822	9207.32

表1：速调管振荡模测量数据

该振荡模中心频率，电子调谐范围为。

观察传输式腔的谐振曲线，测量腔的有载品质因数

在信号发生器的电流最大位置的附近调节反射极旋钮，检流计示数非匀速地由小变大再变小，此即为谐振腔的谐振曲线。

测量结果如表2所示：


112	3.778	9216.61
66	3.786	9214.92
66	3.771	9218.09

表2：传输式谐振腔的有载品质因数测量数据

计算的谐振腔的有载品质因数为。

用简便方法测量共振磁场Hr和线宽

电磁铁电流-磁场关系为。测量结果如表3所示。


1	106.5	58.0	75.0	2.227	2.171	2.367	3235.53	272.44
2	110.0	60.0	77.5	2.227	2.139	2.339	3235.53	278.00
3	109.0	57.0	75.0	2.252	2.146	2.334	3270.28	261.32

表3：简便方法测量共振磁场和线宽测量数据

由此，分别给出共振磁场和线宽的平均值，共振磁场，线宽。计算可得回磁比，g因子，弛豫时间。

逐点测绘P−H曲线

测得P−H曲线如图6所示

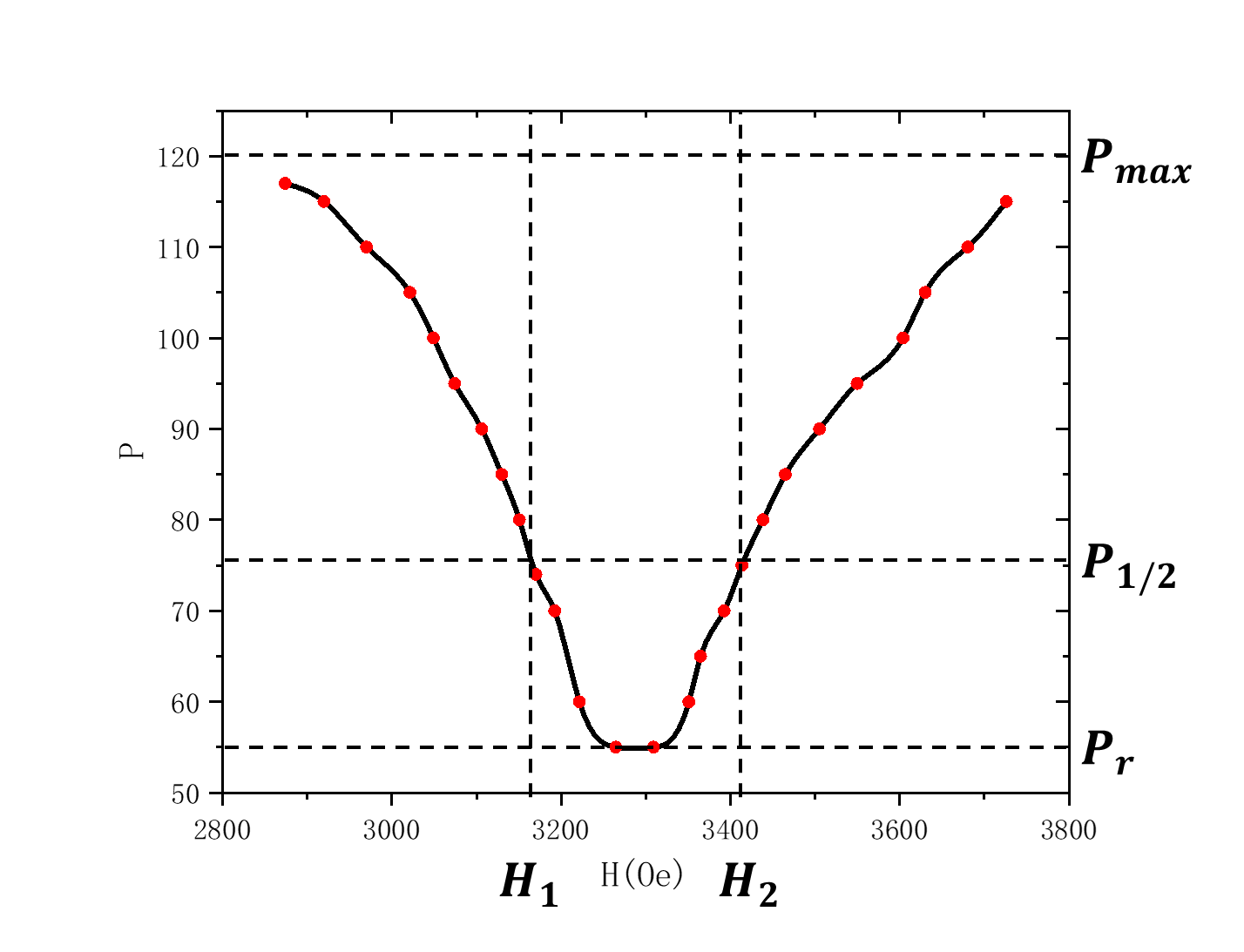
图6：P-H曲线

根据曲线，共振磁场，线宽。计算可得回磁比，g因子，弛豫时间。可以看到两种方法得到的结果大体一致，考虑到仪器误差较大，两者的差异在可接受范围内。

结论

本次实验中，我们观测了反射式速调管的振荡模，确定了一个振荡模的中心频率以及速调管的电子调谐范围，掌握了微波信号发生器的使用方法。我们观测了传输式谐振腔的谐振曲线，测量了其有载品质因数，了解了谐振腔的工作特性。我们观测了谐振腔中多晶铁氧体小球的铁磁共振效应，通过测量共振磁场和P−H曲线线宽，得到了回磁比，g因子和弛豫时间，加深了对于铁磁共振效应的理解。

参考文献

[1] ÜNLÜMS,STRITES. Resonant cavity enhanced photonic devices[J]. Journal of Applied Physics, 1995, 78(2): 607-639.

[2] ÜNLÜMS,STRITES. Resonant cavity enhanced photonic devices[J]. Journal of Applied Physics, 1995, 78(2): 607-639.

[3] GILMOURJRAS. Microwave tubes[J]. Dedham, 1986.

[4] BASUB,DATTAS. Microwave tubes and applications[J]. Journal of Electromagnetic Waves and Applications, 2017, 31(17): 1771-1774.

[5] MOTZ H. An analysis of klystron reflector performance[J]. Journal of the Institution of Electrical Engineers-Part III: Radio and Communication Engineering, 1948, 95(36): 295-301.

[6] 荀坤吴思成. 近代物理实验(第四版)[M]. 高等教育出版社,2015.

Supplement：思考题

谐振腔的谐振频率为，对应波长为。波导波长为。则腔长为。样品放置位置应满足电场为，因此应放置在驻波波节处，即距离谐振腔端面整数个半波长的位置。
- 远离共振点时，调节衰减器，使检波电流为一个较小的值，记录此时的衰减量和检波电流。
- 共振点处，降低衰减器的衰减，使检波电流恢复到，记录此时的衰减量。
- 利用公式计算出，将衰减器衰减量调至算出的，朝两个方向调节磁场，使检波电流恢复到，对应的两个磁场之差即为线宽。
- 改变衰减量，调节磁场，使检波电流恢复到，逐点测量，即可得到曲线。