摘要： 测定半导体的电阻率和霍尔系数，可以获知其基本电磁特性，这有助于我们了解其导电机制以及验证固体物理的结论。本实验将这一办法应用到了型硅半导体的研究中，通过测定硅片样品的电阻率和霍尔系数，验证其的导电特性。具体而言，本实验利用四线范德堡法测量了从室温至约150°C范围内p型硅的电阻率和霍尔系数，获得并分析了该温度范围内电阻率和霍尔系数随温度的变化关系，并按照变化趋势的不同将p型硅半导体的导电特性划分出了几个明显区间，验证了固体物理对掺杂半导体的导电机制的预测，并进一步给出了所用硅片样品的带隙宽度∼eV

关键词：半导体，p型硅，能带理论，电阻率，霍尔效应

引言

半导体有别于导体和绝缘体，是一种导电性能随外界条件（如电磁场、温度等）变化强烈的电学材料。早在19世纪初，意大利物理学家Guglielmo Marconi就提出了半导体的概念^[1]，人们便观察到了半导体的若干非同寻常的性质，特别是其电阻可能随温度增高而下降的特点与寻常的导体截然不同。这样的特点让半导体在电子学、材料学等领域有着不可或缺的价值，同时也吸引了固体物理学家对其研究的兴趣。

1878年，Edwin Herbert Hall发现，施加了外加垂直磁场的通电导体会在第三个垂直方向上积累稳定的电压，而电压的正负则取决于载流子的类型，此即霍尔效应。简单的电磁学推导可以用正负电荷的载流子定向漂移解释霍尔电压的形成，但是这与半导体中应当只有游弋的自由电子才能形成电流的常识矛盾。

这一疑惑直到20世纪中期才被充分发展的量子力学和固体理论所解释：Felix Bloch提出了描述电子在周期性晶体中的运动的波函数形式^[2]，Charles Thomson Rees等人使用Bloch函数解释了导体和半导体的导电特性，同时预言了含有P掺杂的硅晶体在低温、室温和高温下霍尔系数和电导率的差异和变化。^[3]

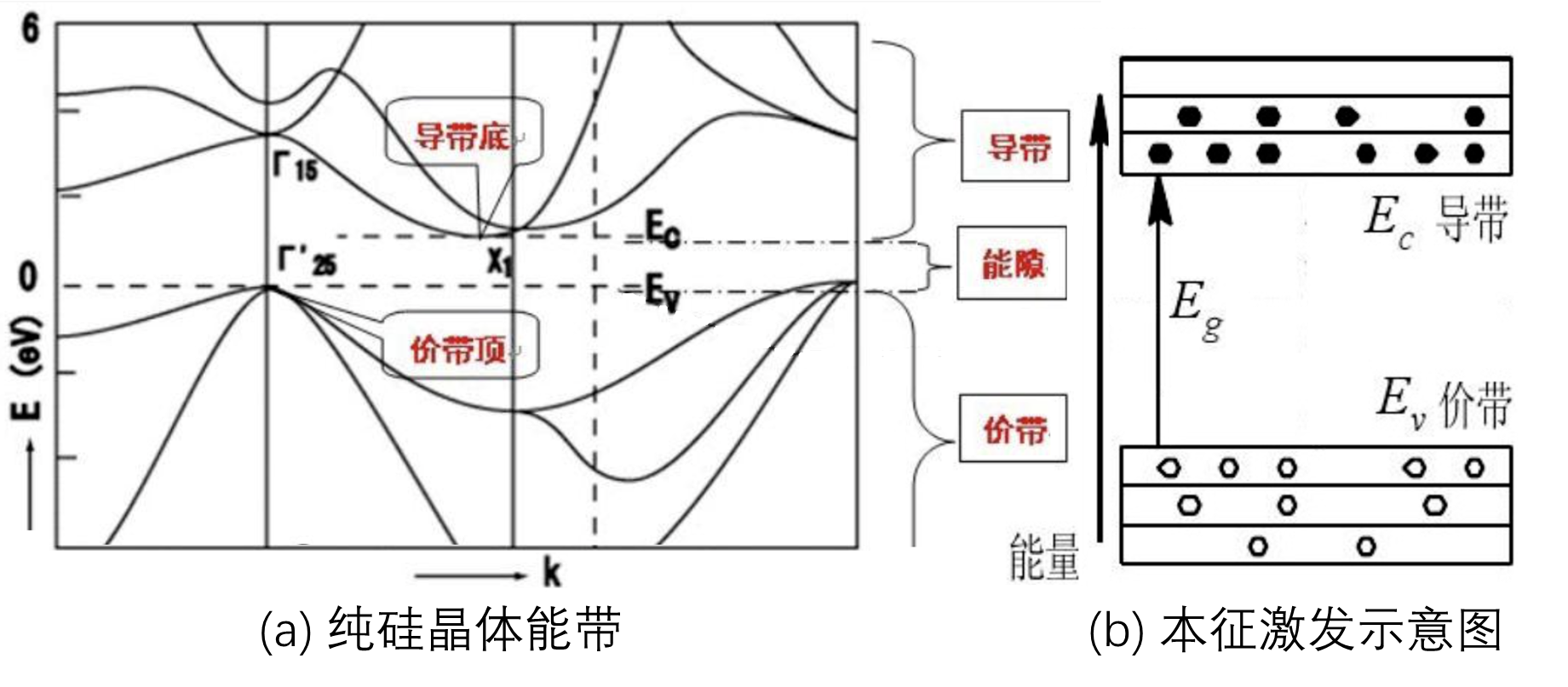
图1：半导体的Si的特性

如图1(a)所示是纯硅晶体的能带图，利用晶体内周期性的势条件可以计算出电子在其中运动的所有本征态。按照能量由小到大将本征态排列，则会得到导带和禁带依次排列的结构，被电子填满的价带构成了相空间的费米面。此时价带内的电子的动量不能连续变化，因此不能因为受外加电场的作用而作定向运动，不导电。而当温度升高，电子的热运动开始允许电子跨越能隙而被激发到能量更高的空导带，动量连续变化而可以导电，如图1(b)所示^[4]。

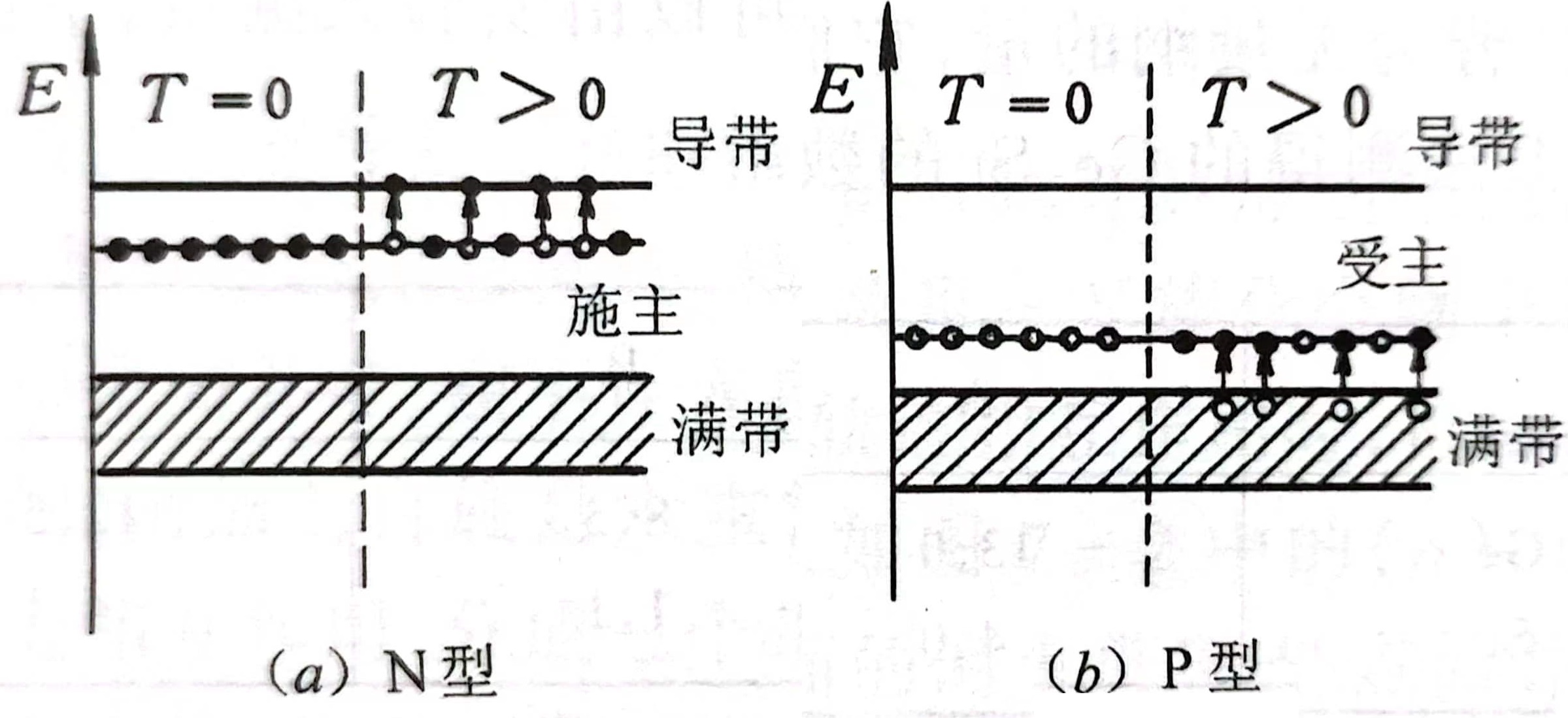
如图2所示是N掺杂硅晶体和P掺杂晶体的能带图，由于杂质原子是通过取代正常原子而进入晶格的，晶体的能带结构仍和纯硅晶体一致。对于N掺杂硅中的五价原子，如磷、砷等，由于多一个电子，使得其费米面相比硅更高，但仍低于导带底。此时，只需克服更小的能隙就能将N型原子的电子激发到导带中，所以需要的导通温度比纯硅晶体低。^[5]

图2：N型和P型半导体杂质激发示意图

类似N掺杂系统，P掺杂系统中的三价原子，如硼、铝等，由于少一个电子，其费米面相比硅更低。此时对于硅原子的价带电子来说，只要克服更小的能隙就能激发到P型原子的价带中。这时，硅价带中新出现的空穴便可以导电。

由于半导体基质本身电子的热激发，导致价带电子进入导带而导电的，如图1(b)，称为本征导电。由于引入杂质获得额外电子或空穴而导电的，如图2，称为杂质导电。正如上文所讨论的，由于杂质的引入减小了能隙，因此发生杂质导电的特征温度要低于本征导电。

在本实验中，我们将通过大范围地调节温度来，测量P掺杂半导体硅的霍尔系数和电导率随温度的变化，来检验这一理论的正确性，同时计算相关参数。

理论

电导率随温度的变化关系

在半导体中，电导率主要与载流子浓度和迁移率这两个参数成正比，其随温度的变化关系总体可分为三个区间：

杂质部分电离的低温区。在这一区间电导的变化趋势主要由杂质决定。由于杂质的电离随温度升高而增强，载流子浓度提高。另一方面，由于杂质散射随温度升高而减小，迁移率也随之增加。综合来看，在低温区电导率随温度升高而增加。
杂质电离饱和区。在这一区间电导的变化趋势主要由晶格决定。一方面，在这一区间杂质已全部电离，载流子浓度基本不变。另一方面，随温度升高，晶格振动增强，根据能带理论，周期势场的影响已被归入能带上电子的有效质量，而我们熟悉的散射是由非周期势场例如晶格振动所引起的，因此散射随温度升高而增强。同时，晶格的集体振动对应于一定的声子模式，随温度升高激发的声子数量增加，载流子与声子相互作用的几率也随之提高，从而导致散射随温度升高而增强，迁移率随之下降。

在这一温度区间，电导率与空穴迁移率成正比，相应的有：
$\left(\mu_{Lp}\right)_T=\left(\mu_{Lp}\right)_{300}\frac{\sigma_T}{\sigma_{300}}$
上式中和为300K下的空穴迁移率和电导率。通过测量电导率，并根据300K下的迁移率和电导率可以得到迁移率随温度的变化关系。事实上，这时迁移率和温度之间存在幂次关系：
$\left(\mu_{Lp}\right)_T=AT^{-x}$
本征激发的高温区。这一区间本征激发显著，成对地产生电子、空穴，电子浓度n和空穴浓度p均随温度指数增大，迁移率依然为下降趋势，但仅仅是幂次下降，根据Morin等人的研究，迁移率随温度增加满足如下的变化行为：
$\mu_{Ln}=4.0\times10^9T^{-2.6}(cm^2/V\cdot s)$ $\mu_{Lp}=2.5\times10^8T^{-2.3}(cm^2/V\cdot s)$
因此综合的效果是电导率增大。

我们可以进一步考虑本征激发占主导作用的阶段，首先室温对应的热激发能量约为：

$k_BT_0\approx0.03eV$

其中为玻尔兹曼常量，而半导体的能隙约为量级，因此能隙远大于室温诱导的热激发，可以用麦克斯韦-玻尔兹曼分布来描述粒子数按能量的分布：

$a_n(\epsilon)\sim \begin{cases} \exp{\left(\frac{\epsilon_F-\epsilon}{k_BT}\right)}~~~~~~~~~~~~~~~(\epsilon>E_c)\\ \exp{\left(\frac{\epsilon-\epsilon_F}{k_BT}\right)}~~~~~~~~~~~~~~~(\epsilon<E_v) \end{cases}$

其中和分别是导带的能量下界和价带的能量上界，对其进一步积分可得：

$n\cdot p=AT^3\exp{\left(-\frac{E_g}{k_BT}\right)}$

也就是说，可以利用本征激发区间的电导率随温度变化关系来计算得到半导体能隙的大小：

$E_g=\frac{k_B\Delta\ln{(npT^{-3})}}{\Delta(1/T)}$

霍尔系数随温度的变化关系

在半导体中，霍尔系数主要与载流子浓度和类型这两个因素有关，理论上可以证明霍尔系数与它们之间的关系为：

$R_H=\frac{3\pi(p\mu_{Lp}^2-n\mu_{Ln}^2)}{8q(q\mu_{Lp}+n\mu_{Ln})}=\frac{3\pi(p-nb^2)}{8q(p+nb)^2}$

其中为两种载流子迁移率的比值。霍尔系数随温度的变化关系总体也可分为三个区间：

温度较低的杂质电离饱和区。在这一区间，杂质都已电离，因此载流子浓度随温度保持不变，霍尔系数基本不变。
温度继续升高，霍尔系数从正值减小直至达到负的极小值。在这一区间，电子从价带激发到导带，相应的价带上产生一个空穴，形成电子空穴对，电子和空穴二者数目严格相等。但由于电子迁移率比空穴更大，在同一电场作用下电子运动速度比空穴更快，相应地受到更大的洛伦兹力，对霍尔效应的贡献也更多。随着温度升高，激发的电子数目逐渐增多，电子对应的霍尔系数为负，因此随着电子激发，霍尔系数也逐渐减小直至为负并达到极小值。

极值可由式(9)求导并利用载流子浓度之间的守恒关系得到：
$R_{H\text{极值}}=-\frac{3\pi}{8}\frac{1}{N_Aq}\frac{(b-1)^2}{4b}=-R_{H_s}\frac{(b-1)^2}{4b}$
其中为受主杂质浓度，其与电子和空穴浓度之间存在守恒关系。注意这里的恰为电离饱和区的霍尔系数，利用这一特点我们可以估算值。
温度继续升高，本征激发使载流子数目指数增大并且增大到远大于受主杂质浓度时，，此时根据式(9)可知霍尔系数将指数减小直至趋于0。

实验装置

本实验中所用的仪器包括BWH-I型霍尔效应测量仪，铜-康铜热电偶温度计，PZ93A型直流数字电压表，I型-PMMR永磁魔环以及硅片样品等。实验中利用范德堡法测量样品的电阻率和霍尔系数，样品的示意图如图3所示。这种方法的优点是测量时样品的形状可以随意选择，并且不用考虑接触电阻对测量的影响。利用永磁魔环来调节磁场是为了方便地改变磁场方向而不改变磁场强度，只要样品置于永磁魔环中央就可满足这一需求。热电偶温度计的电压-温度关系由下式给出：

$\varepsilon/mV=at+bt^2+ct^3~~~~~~~~~(t/\text{°}C=T/K-273)$

其中，。

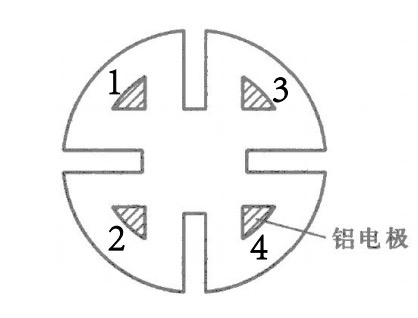
图3：实验中所用的p型硅样品示意图

图3：实验中所用的p型硅样品示意图^[6]

根据实验中在不同温度下测得的在有无磁场、磁场正负、电流正向与反向等不同条件下的电压来计算电阻率和霍尔系数，计算式由以下二式给出：

$\rho=\frac{\pi d}{\ln{2}}\frac{V_I-(-V_I)+V_{II}-(-V_{II})}{4i}f$ $R_H=\frac{d}{B}\frac{V_{III}(+I,+B)-V_{III}(+I,0)+V_{III}(-I,-B)-V_{III}(-I,0)}{2i}$

其中和分别是在1和2端通电流测量3和4端的电压，以及2和3端通电流测量1和4端的电压，它们的负值代表将电流反向时测量得到的电压。是在1、3端通电流测量2、4端的电压，改变实验条件，即有无磁场、磁场和电流的正向反向，测量，可以较好地消除埃廷斯豪森效应、能斯特效应、里纪-勒杜克效应等热磁副效应，这是我们在常规的霍尔效应实验中已经熟悉的方法。

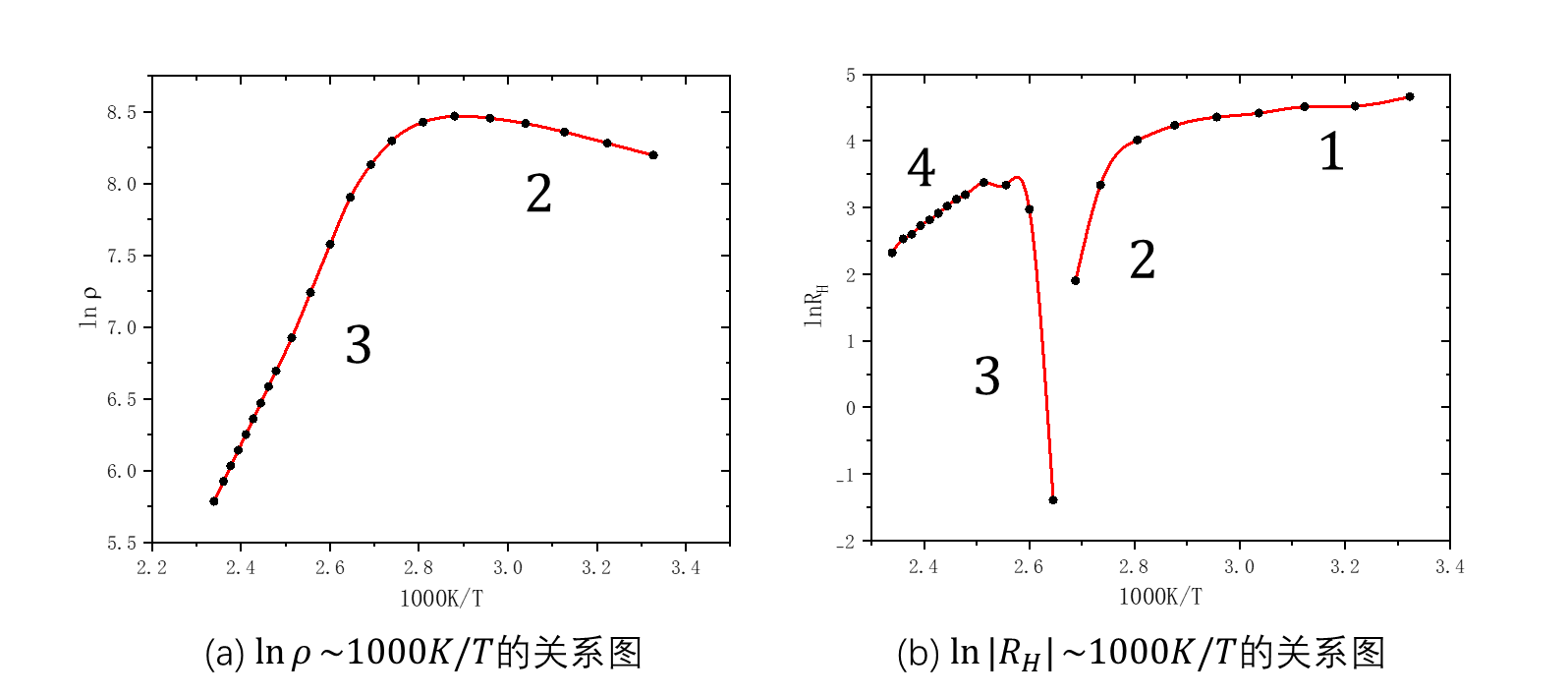
结果与讨论

测量电阻率和霍尔系数随温度的变化关系

实验时，通过霍尔效应测量仪设置不同温度，等待样品温度稳定，读出温度计示数，改变电压旋钮指向、电流方向和磁场方向，保持电流大小为，依次读出，，，，，，，。

实验中，测量了从室温(23.44°C)到154.31°C下的电阻率和霍尔系数。通过样品的电流取为，用一恒流源提供。由于样品降温相对加热来说慢得多，因此为了保证测量的方便准确，防止意外情况，先在室温下做简单检验，判断电阻率和霍尔系数是否在合理区间。室温下测得电阻率，霍尔系数。与实验室给出的参考值和比较接近。因此认为实验条件正常，参数处于合理范围，开始进行接下来升温的测量。

实验中发现温度的弛豫时间较长，且仪器的反馈有明显滞后性，在每次设定温度后会有先升温再降温的过程。若每次都等待温度彻底稳定，时间就过长了；并注意到温度在达到最大值附近的变化会较为缓慢，因此在温度达到最大值附近时迅速完成测量，并记录初始温度和测量结束的温度。从实测数据来看，精度在可接受的范围内。

做出图像如图4所示。与理论预言的形状几乎完全一致。注意到，电阻的曲线和电导的是相反的。

图4：电阻率和霍尔系数随温度变化的关系图

图4(a)中2的部分和(b)中1的部分对应为杂质的电离饱和区，温度范围大致为，当测量的温度达到最大时，，有方程(9)我们不难看出，此时应有电子浓度大于空穴的浓度，所以此时已经完全进入了本征态范围。

空穴迁移率随温度的变化关系

$图5：$\lnμ_{Lp} − \ln T$的线性关系拟合$

图5：lnμ_Lp−lnT的线性关系拟合

我们下面利用电阻率的实验数据内插(外插)出300K下的电阻率，就可以通过式(1)和计算出杂质电离饱和区内的空穴迁移率。使用matlab中的spline函数内插出室温(300K)下的电阻率为：

$\rho_{300}=3608.2\Omega\cdot cm$

我们将计算出来的数据同方程(2)进行拟合，并于Morin给出的结果进行对比，拟合图如图5所示。从图中给出的数据我们可以给出拟合的参数分别为：

$\begin{cases} \ln{A}=18.995\pm 0.86\\ x=2.25\pm 0.15 \end{cases}$

即：

$\begin{cases} A=(0.75\sim 4.20)\times 10^8\\ x=2.25\pm 0.15 \end{cases}$

和Morin的结果相差不大，但是因为实验是在室温时进行的，已经处于杂质电离饱和区和本征激发区的交界，此处电阻率几乎达到极大值，并不完全满足公式，因此用这些数据拟合只能得到一个带有估计性质的结果。如果想要得到进一步精确的结果来验证Morin的结果是否正确，需要把样品的温度降低到室温以下进行测量。

估算b值

当温度逐渐升高时，价带上的电子开始激发到导带，若温度继续升高，更多的电子将会从价带激发到导带，使，进而使，随后将会达到一个极值，即当时，有方程(10)所述的关系。在图4(b)中我们给出 $极值$ 。将这些数据代入方程(10)可以得到的值：

$b=1-2\frac{R_{H\text{极值}}}{R_{Hs}}+\sqrt{\left(1-2\frac{R_{H\text{极值}}}{R_{Hs}}\right)^2-1}\approx2.897$

利用Morin的结论有，将极值处的温度代入可得。对于与之间产生的误差，一方面可能是寻峰拟合对极值点位置判断出现误差，导致极值温度出现偏离，带来了一部分误差，另一方面可能是测量霍耳系数带来的误差。在测量过程中能够注意到，旋转永磁魔环会使样品温度的读数产生一个瞬间的跳动，这个过程或许会改变样品的状态。

杂质浓度、空穴浓度与电子浓度

通过插值法我们得到在时的电阻率为。于是可算得杂质浓度：

$N_A=p_s=\frac{\sigma_{300}}{q(\mu_{Lp})_{300}}=\frac{1}{\rho_{300}q(\mu_{Lp})_{300}}=3.6\times10^{12}cm^{-3}$

在最高温度处°C，电阻率为，根据：

$\sigma=q(p\mu_{Lp}+n\mu_{Ln})$

以及载流子浓度之间的守恒关系，可以解出：

$\begin{cases} p=\left(\frac{\sigma}{q\mu_{Lp}}+bN_A\right)/(b+1)=2.62\times10^{13}cm^{-3}\\ n=\left(\frac{\sigma}{q\mu_{Lp}}-N_A\right)/(b+1)=2.98\times10^{13}cm^{-3} \label{4.7} \end{cases}$

可见电子和空穴的浓度都比杂质浓度高出一个数量级，的条件基本得到满足, 表明本征激发已经比较完全了。这也验证了我们之前的说法。

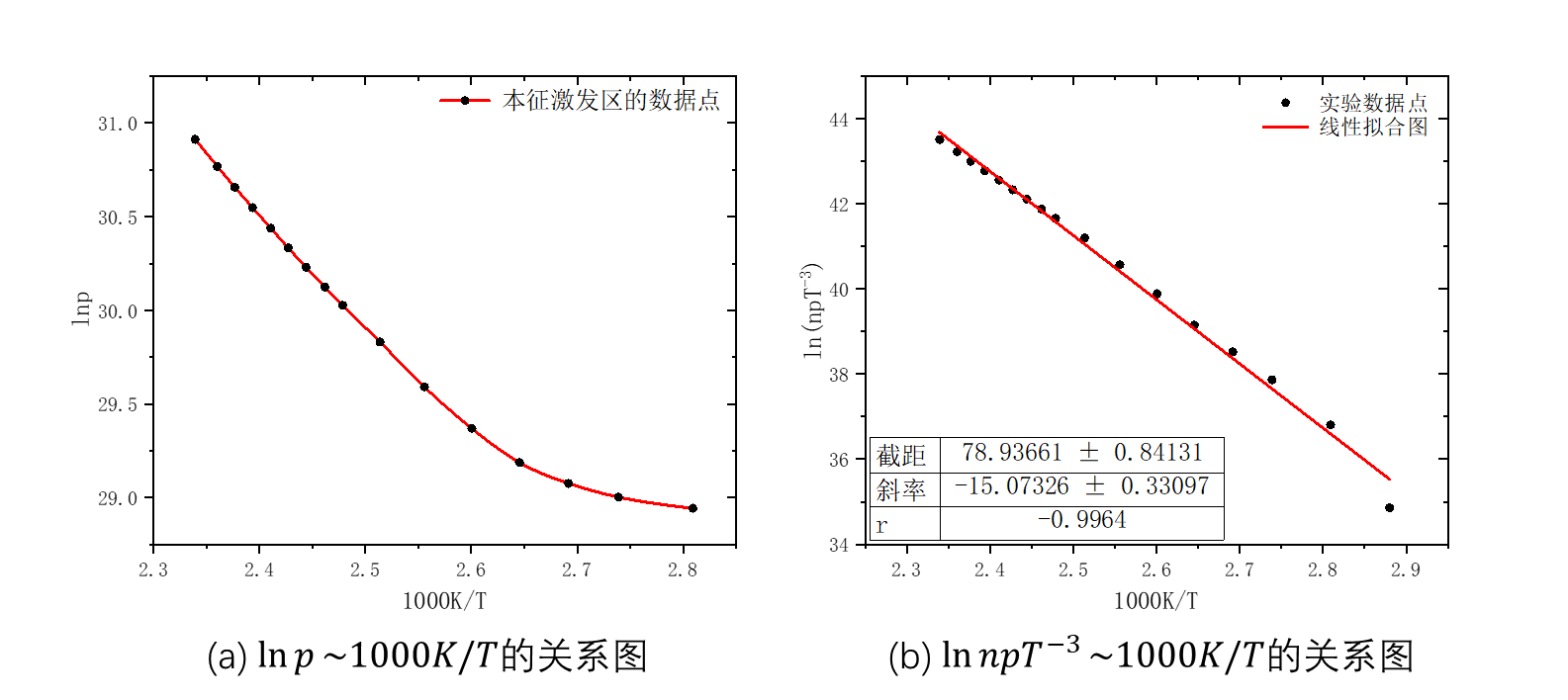
载流子浓度及禁带宽度计算

同样地，利用方程(20)计算出本征激发区域内的并做出曲线，如图6(a)所示。然后计算随的变化关系，并且取温度较高时比较符合线性的部分进行拟合，如图6(b)所示。

图6：载流子浓度和温度的关系图及相关拟合

得到的拟合结果为：

$\begin{cases} k=-15.07\pm 0.33\\ |r|=0.9964 \end{cases}$

可见和之间满足较好的线性关系。再由拟合得到的斜率即可得到p型硅的能隙为：

$E_g=1000k_B||k=1.299\pm0.010eV$

比书中给出的标准值1.12eV略微偏大。但书上的标准值是在300K下测得，随温度升高晶格振动加剧可能会对电子能级有一定的影响。当然本实验本身也存在一些偶然误差，如果想进一步提高精度，应该使用更加高效的温控系统和更加精确的电压测量系统。

评估对于实验结果的影响

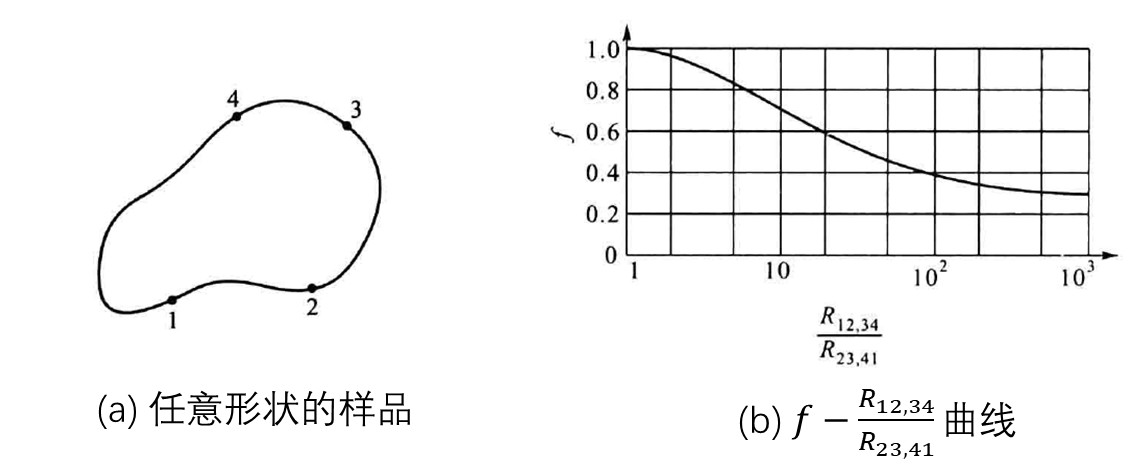
图7：测量中采用模型的计算方法

我们在实验中采用了任意形状、厚度为d、中间没有空洞的薄样品电阻率的计算公式，如图所示，图中1、2、3、4分别代表四个接触点，可以证明电阻率为：

$\rho=\frac{\pi d}{\ln{2}}\frac{R_{12,34}+R_{23,41}}{2}f$

其中，

$R_{12,34}=\frac{V_4-V_3}{i_{12}}~~~~~,~~~~~R_{23,41}=\frac{V_1-V_4}{i_{23}}$

另外，方程(23)中的参数由下面的方程给出：

$\cosh{\left[\frac{R_{12,34}/R_{23,41}-1}{R_{12,34}/R_{23,41}+1}\frac{\ln{2}}{f}\right]}=\frac{1}{2}\exp{\left(\frac{\ln{2}}{f}\right)}$

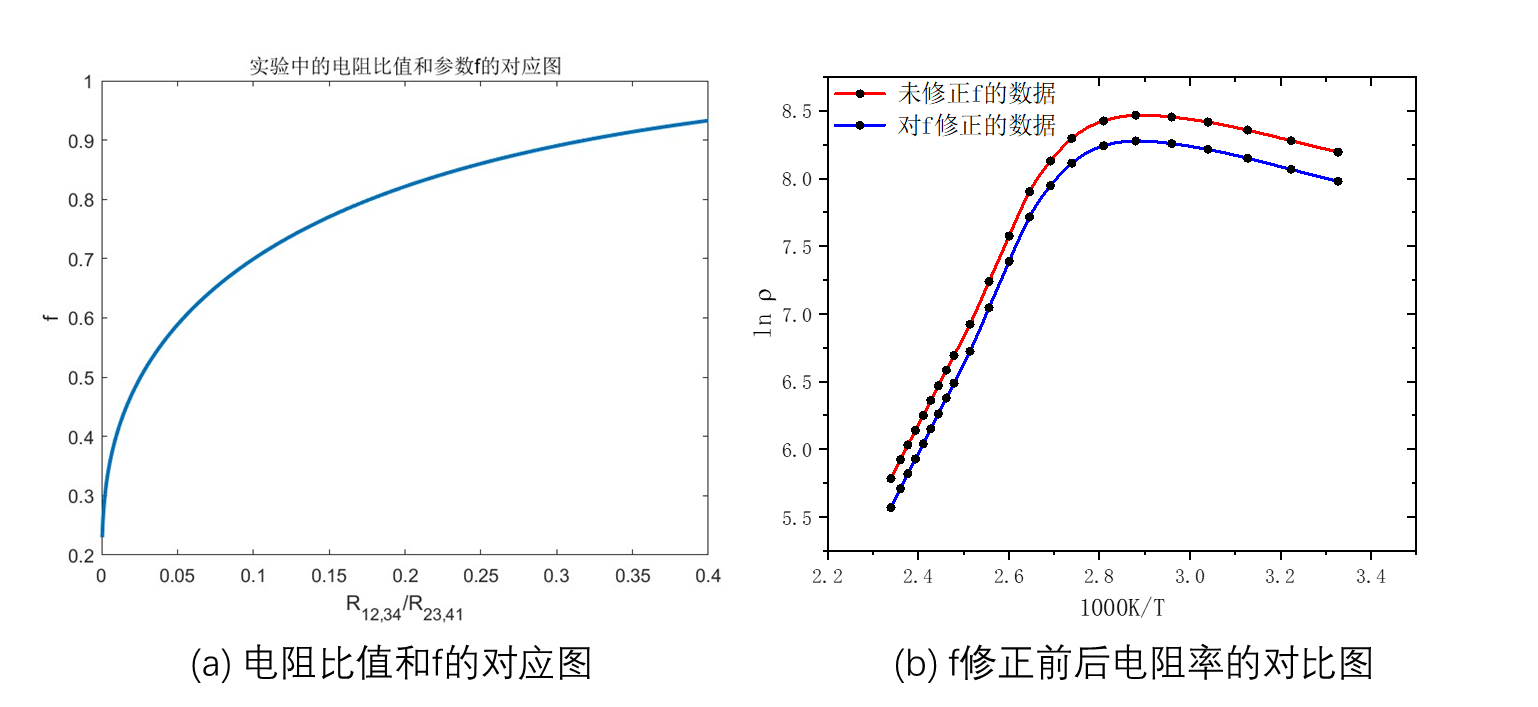
我们给出对f进行修正后的实验数据同未进行修正的对比图，如下图所示

图8：f的修正对实验结果是否有很大的影响

可以看出f的修正与否对于实验中电阻率测量的影响基本保持在0.02的范围内，这个误差对于我们的实验来说是可以接受的。所以上述的实验结果可以认为不受f修正与否的影响。

结论

本实验测得了室温至154.3°C范围内p型硅的电阻率与霍尔系数随温度的变化关系，发现样品的性质随温度变化时，存在几个变化趋势明显不同的区间，并验证了固体物理中的论。实验结果表明，实验室提供的的p型硅样品在室温下处于杂质的电离饱和区和本证激发区的交界，随后测得的电阻率和霍尔系数随温度变化的规律与固体物理的预测一致。

在此基础上，我们估算了p型硅的杂质浓度和本征激发较为充分时的载流子浓度，两者分别和量级。进一步，根据霍尔系数的极小值给出了电子、空穴迁移率比例b的估计值，最终测得带隙宽度约为1.299eV。

但是由于室温下p型硅样品在室温下已经处于杂质的电离饱和区和本征激发区的交界，因此对于空穴迁移率与温度之间的幂次关系的计算是不准确的，结果与文献相差较大，需要进一步的降温测量来验证幂次关系。

参考文献

[1] DYLLA H F, CORNELIUSSEN S T. John ambrose fleming and the beginning of electronics[J/OL]. Journal of Vacuum Science and Technology, 2005, 23: 1244-1251. https://api.semanticscholar.org/CorpusID:93105247.

[2] BLOCHF. ber die quantenmechanik der elektronen in kristallgittern[J]. Eur. Phys. J. A, 1929, 52(7-8): 555-600.

[3] DE L. KRONIG R, PENNEY WG. Quantum mechanics of electrons in crystal lattices[J]. Proc. R. Soc. Lond. A Math. Phys. Sci., 1931, 130(814): 499-513.

[4] 黄昆. 固体物理学[M]. 高等教育出版社,2012.

[5] KITTEL C. Introduction to solid state physics[M]. 化学工业出版社, 2005.

[6] 吴思成、荀坤. 近代物理实验(第四版)[M]. 高等教育出版社,2015