前言

因为是本学期在学的课程，马上要期中考试了，打算尝试通过写blog的方式来复习一下。所以这部分现在不重要，后面我会好好写这部分的QWQ

函数的渐近界

基本定义和定理

$\qquad$ 在算法分析中的函数通常是定义在自然数集合上的函数$f:\mathbb{N}\to\mathbb{N}$，并且函数$f(n)$通常为非负的。我们在学习高数中的极限时，通常会描述某个非负函数阶数更大，这个阶数实际上就是我们现在要说的函数的渐近界。

定义1 假设$f$和$g$是定义域为自然数集$\mathbb{N}$上的函数

若存在正数$c$和$n_0$使得对一切$n\ge n_0$有$0\le f(n)\le cg(n)$成立，则称$f(n)$的渐进上界是$g(n)$，记作$f(n)=O(g(n))$

若存在正数$c$和$n_0$使得对一切$n\ge n_0$有$0\le cg(n)\le f(n)$成立，则称$f(n)$的渐进下界是$g(n)$，记作$f(n)=\Omega(g(n))$

若对于任意正数$c$都存在$n_0$，使得对一切$n\ge n_0$时有$0\le f(n)\lt cg(n)$，则记作$f(n)=o(g(n))$

若对于任意正数$c$都存在$n_0$，使得对一切$n\ge n_0$时有$0\le cg(n)\lt f(n)$，则记作$f(n)=\omega(g(n))$

若$f(n)=O(g(n))$且$f(n)=\Omega(g(n))$，则记作$f(n)=\Theta(g(n))$

实际上，在记忆时，可以将 $O$ 、 $\Omega$ 、 $o$ 、 $\omega$ 和 $\Theta$ 看成一种函数之间的比较，其中， $O$ 代表 $\le$ ， $o$ 代表 $\lt$ ，$\Omega$ 代表 $\ge$ ，$\omega$ 代表 $\gt$ ，最后， $\Theta$ 代表 $=$ ，这样记忆就会更加方便。通过极限来判断函数之间的关系是更加直观和数学化的：

定理1 (极限判定) 设$f$和$g$是定义在自然数集$\mathbb{N}$上的函数

如果$\lim_{n\to\infty}\frac{f(n)}{g(n)}$存在，并且等于某个常数$c>0$，那么$f(n)=\Theta(g(n))$。

如果$\lim_{n\to\infty}\frac{f(n)}{g(n)}=0$，那么$f(n)=o(g(n))$。

如果$\lim_{n\to\infty}\frac{f(n)}{g(n)}=+\infty$，那么$f(n)=\omega(g(n))$。

除了数院的人，真的有人care怎么证明吗QWQ

定理2 (传递原理) 设$f$，$g$，$h$是定义在自然数集$\mathbb{N}$上的函数

如果$f=O(g)$且$g=O(h)$，那么$f=O(h)$。

如果$f=\Omega(g)$且$g=\Omega(h)$，那么$f=\Omega(h)$。

如果$f=\Theta(g)$且$g=\Theta(h)$，那么$f=\Theta(h)$。

定理3 (合并原理) 设$f$和$g$是定义在自然数集$\mathbb{N}$上的函数，若对于某个其他的函数$h$，有$f=O(h)$和$g=O(h)$，那么$f+g=O(h)$

基本函数

$\qquad$ 为了更加清楚的了解函数的阶数，我们不妨先重新认识一些我们熟知的函数，下面我们将分别按照多项式函数、对数函数、指数函数、阶乘函数，以及取整函数的顺序进行讨论。

多项式函数

$f(n)=a_0+a_1 n+\cdots+a_d n^d$称为$d$次多项式，其中$a_d\neq0$。通过定理1不难证明，这类函数有$f(n)=\Theta(n^d)$。值得注意的是，一些函数中可能$d$并不是整数，例如整数乘法运算的时间复杂度$O(n^{1.59})$，甚至有可能含有别的函数，但是只要另一个函数在$n\to\infty$时可以被忽略掉，例如归并排序算法时间复杂度$O(nlogn)$，那么我们也称其为多项式函数。

对数函数

对数函数$\log_b n$的值等于$x$当且仅当$b^x=n$。对数函数有一个十分重要的性质在比较函数阶数时十分常用：

$a^{\log_bn}=n^{\log_ba}$

即当对数在指数上时，底数可以和对数中的底数互换，很大程度上可以帮助我们将一个看不懂是什么的函数转化为一个多项式函数。当然这个式子的证明可以两边同时对b取对数，这时我们将指数部分放到对数外，就会发现两边是相同的。对数函数是一类增长十分缓慢的函数，可以证明他比任何幂函数$n^\alpha~~(\alpha>0)$的阶数都低，具体可以描述为：

定理4 对于$b>1$和每个$\alpha>0$，有$\log_bn=o(n^\alpha)$。

另外，对于不同底的对数函数，他们的阶数都是相同的，他们之间只差一个常数，即：

$\log_an=\frac{\log_bn}{\log_ba}$

对于不同的$a$和$b$，有$\log_an=\Theta(\log_bn)$。正是由于这个性质，我们通常使用以2为底的对数($\log n$)描述一个问题。

指数函数

算法分析中的指数函数一般不收敛，即形如$f(n)=r^n$，其中$r$为某个大于1的常数。指数函数是一个飞速增长的函数，他比任何多项式函数增长都快：

定理5 对每个$r>1$和每个$d>0$，有$n^d=o(r^n)$。

不用于对数函数，对于不用的$r$和$s$，指数函数$r^n$和$s^n$的阶数是不同的，底数越大，阶数越高。

阶乘函数

$f(n)=n!$是一类增长极快的函数，在具体处理这类函数时，我们一般会使用$\Gamma(n)$函数的渐进表达式，即Stirling公式：

$n!=\sqrt{2\pi n}\left(\frac{n}{e}\right)^n\left(1+\Theta(\frac1n)\right)$

我们通过一个例子展示具体使用时的方法，我们来证明一下 $\log(n!)=\Theta(n\log n)$ ，考虑使用定理1：

$\begin{align} \lim_{n\to+\infty}\frac{\log(n!)}{n\log n}&=\lim_{n\to+\infty}\frac{\ln(n!)}{n\ln n}\\ &=\lim_{n\to+\infty}\frac{\ln\left(\sqrt{2\pi n}\left(\frac ne\right)^n\left(1+\frac{c}{n}\right)\right)}{n\ln n}\\&=\lim_{n\to+\infty}\frac{\ln\sqrt{2\pi n}+n\ln\frac{n}{e}}{n\ln n}=1 \end{align}$

所以在使用时，可以设一个常数$c$直接代入表达式中，在$n\to+\infty$时这种假设总是正确的，其实更简化的时直接扔掉后面的一项，在$n$极大时，$1/n$总是比不过$1$的。另外还应该记住两个关系：

$n!=o(n^n)~~~~~~~~~~~\text{阶乘函数的上界}$ $n!=\omega(2^n)~~~~~~~~~~~\text{阶乘函数的下界}$

取整函数

在某些涉及分治的程序中，时间复杂度会有所谓的取整函数，即$\lfloor x\rfloor$和$\lceil x\rceil$，分别称为下取整和上取整，也称为底函数和顶函数，其中$\lfloor x\rfloor$表示小于等于$x$的最大整数，$\lceil x\rceil$表示大于等于$x$的最小整数。例如：$\lfloor3.4\rfloor=3$；$\lceil3.4\rceil=4$。取整函数具有以下性质：

$x-1<\lfloor x\rfloor\le x\le\lceil x\rceil<x+1$
$\lfloor x+n\rfloor=\lfloor x\rfloor+n$，其中$n$为整数
$\lceil\frac{n}{2}\rceil+\lfloor\frac{n}{2}\rfloor=n$，其中$n$为整数
$\lceil\frac{\lceil\frac{n}{a}\rceil}{b}\rceil=\lceil\frac{n}{ab}\rceil$，$\lfloor\frac{\lfloor\frac{n}{a}\rfloor}{b}\rfloor=\lfloor\frac{n}{ab}\rfloor$，其中 $n,a,b$ 都是整数

总结

我们以一道例题作为这部分的收尾，这部分最常见的习题就是给一堆函数，让按阶数进行排序，例如：

例题1 给定一些函数，请将他们按照渐近界从高到低进行排序，如果一个函数$f(n)$和$g(n)$的阶数相等，则表示为$f(n)=\Theta(g(n))$

函数：$\log^2n$，$1$，$n!$，$n2^n$，$n^{1/\log n}$，$(3/2)^n$，$\sqrt{\log n}$，$(\log n)^{\log n}$，$2^{2^n}$，$n^{\log\log n}$，$n^3$，$\log\log n$，$n\log n$，$n$，$2^{\log n}$，$\log n$，$\log(n!)$。

解决办法是首先摘出一些熟悉的所谓的基本函数，再将其余的与这些基本函数进行对比：

有几个比较简便的结论可以记忆：（我就不写的特别严格了）

$\log^\alpha n<n$，其中$\alpha$是一个常数

$(\log n)^{\log n}=n^{\log\log n}$，这个东西大于任何多项式函数，小于任何指数函数（证明就是用定理1就好）

对于其他情况，尽可能的通过定理1进行验证，不要基于直觉进行判断，因为一般会出一些反直觉的题目

给出例题1的答案，按从大到小的顺序分别为：

$2^{2^n}$，$n!$，$n2^n$，$(3/2)^n$，$(\log n)^{\log n}=n^{\log\log n}$，$n^3$，$\log(n!)=\Theta(n\log n)$，$n=\Theta(2^{\log n})$，$\log^2 n$，$\log n$，$\sqrt{\log n}$，$\log\log n$，$n^{1/\log n}=\Theta(1)$。

求和的方法

等差数列、等比数列和调和级数

对于等差数列$\{a_k\}$，等比数列$\{aq^k\}$和调和级数$\{1/k\}$，其求和公式可以写成：

$\sum_{k=1}^n a_k=\frac{n(a_1+a_n)}{2}$ $\sum_{k=0}^n aq^k=\frac{a(1-q^{n+1})}{1-q};~~~~\sum_{k=0}^n x^k=\frac{1-x^{n+1}}{1-x}$ $\sum_{k=1}^n\frac{1}{k}=\ln n+O(1)$

$O(1)$的部分实际上是欧拉常数$\gamma$。这三个公式能够帮我们解决绝大部分的求和问题，所以遇到求和问题时首先观察形式上是否满足这样三个函数形式。

裂项和错位相减法

当我们面对例如 $\sum_{k=1}^{n-1}\frac{1}{k(k+1)}$ 形式的求和时，就可以选择裂项法进行计算了，这时：

$\sum_{k=1}^{n-1}\frac{1}{k(k+1)}=\sum_{k=1}^{n-1}\left(\frac{1}{k}-\frac{1}{k+1}\right)=1-\frac{1}{n}$

当然对于求和表达式 $\sum_{t=1}^{k}t2^{t-1}$ 进行求和时，不难发现这是一类等差乘等比的求和，一般思路是通过公比相减，例如上述的求和，我们可以假设求和最终值为$y$，通过$2y-y=y$的方法将求和化简：

$2y-y=\sum_{t=1}^k t2^t-\sum_{t=1}^k t2^{t-1}=k2^k-1+\sum_{t=1}^{k-1}t2^t-\sum_{t=1}^{k-1}(t+1)2^t=(k-1)2^k+1$

函数化积分法

对于刚刚的例题，等差乘等比的形式还可以使用函数化后积分的方式进行计算，我们还以上面的求和为例，我们可以假设函数$f(x)=\sum_{t=1}^k tx^{t-1}$，不难看出$f(2)$就是所求和的解。连续函数具有逐项求积分的性质，所以我们可以找到一个$f(x)$的原函数$F(x)=\sum_{t=1}^k x^t$，这个函数就是一个等比数列求和，我们可以给出它的结果为$F(x)=\frac{x(1-x^k)}{1-x}$，我们这时在对其求导使其回到$f(x)$的形式，再代入$x=2$就可以给出求和的解了，答案和上面的是一样的。

放大法和积分估计

放大法可以将序列中所有项替换乘最大的项来估计求和的上界，有时收敛的等比数列也可以将求和上界改为无穷进行求解，这也是一种放大。另外，我们可以通过函数图像分割的方式，使用积分估计一个函数的渐进极限，例如调和级数就可以通过这样的方法求解。不过这两种方法都无法求出确切的解，都是估计一个界，所以就不多赘述了。

递推方程求解方法

定义1 设序列 $a_0,a_1,a_2,\cdots,a_n,\cdots$，简记为$\{a_n\}$，一个把$a_n$与某些$a_i(i<n)$联系起来的等式叫做关于序列$\{a_n\}$的递推方程。

注意要掌握看伪码列出递推方程的能力

迭代法

直接迭代

例如Hanoi塔，给出其伪码：

算法 Hanoi(A,C,n):             #T(n)
if n=1 then move(A,C)
else 
	Hanoi(A,B,n-1)			  #T(n-1)
	move(A,C)
	Hanoi(B,C,n-1)			  #T(n-1)

通过伪码我们可以给出递推方程：

$T(n)=2T(n-1)+1;~~~~T(1)=1$

这时，我们可以直接一步一步进行迭代：

$T(n)=2(2T(n-2)+1)+1=\cdots=2^{n-1}+\cdots+1=2^n-1=O(2^n)$

再如，插入排序：

$W(n)=W(n-1)+n-1;~~~~W(1)=0$

也可以一步一步进行迭代：

$W(n)=W(n-2)+n-2+n-1=\cdots=1+2+\cdots+n-1=\frac{1}{2}n(n-1)=O(n^2)$

换元迭代

以二分归并排序 MergeSort 为例：

$W(n)=2W(\frac n2)+n-1$

当然这个递推方程可以使用主定理来完成，但是也可以使用换元法，令$n=2^k$进行计算

$\begin{align*} W(n)&=2W(2^{k-1})+2^k-1\\ &=2[2W(2^{k-2})+2^{k-1}-1]+2^k-1\\ &=k2^k-2^k+1\\ &=n\log n-n+1 \end{align*}$

所以：

$W(n)=O(n\log n)$

差消迭代

以快速排序为例：

$T(n)=\frac2n\sum_{i=1}^{n-1}T(i)+n-1;~~~~T(1)=0$

由原方程可得：

$nT(n)=2\sum_{i=1}^{n-1}T(i)+n^2-n$ $(n-1)T(n-1)=2\sum_{i=1}^{n-2}T(i)+(n-1)^2-(n-1)$

通过(21)式和(22)式相减可得：

$\frac{T(n)}{n+1}=\frac{T(n-1)}{n}+\frac{2n-2}{n(n+1)}$

在这种情况下进行迭代会更加简便

$\frac{T(n)}{n+1}=2\left[\frac{1}{n+1}+\frac{1}{n}+\cdots+\frac13\right]+\frac{T(1)}{2}-1+O(\frac1n)=\Theta(n\log n)$

归纳验证

在使用迭代法时，在最后都应该进行归纳验证，首先代入$n=1$验证初始值$T(1)$是否正确，然后根据结论给出$T(n)$的表达式，假设其正确并推出$T(n+1)$正确，这样才是完整的迭代过程

迭代模型：递归树

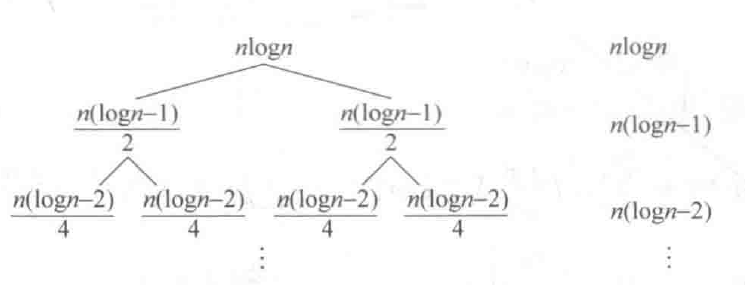
对于形如分治形的递推方程，我们还可以使用递归树来进行计算。例如我们刚刚讨论的二分归并排序，其递推方程为：

$W(n)=2W(\frac{n}{2})+n-1;~~~~W(1)=0$

我们可以构造一个递归树如图1所示：

图1：二分归并排序的递归树

我们最需要知道的就是构建树的层数为$k$，应该有 $n=2^{k-1}$，即$k=\log n+1$。总的时间复杂度就是树种所有节点的值相加：

$W(n)=(n-1)+(\frac{n}{2}-1)\times2+\cdots+1\times2^{k-1}=nk-2^k-1=O(n\log n)$

再举一例：

$T(n)=T(\frac n3)+T(\frac{2n}{3})+n;~~~~T(1)=0$

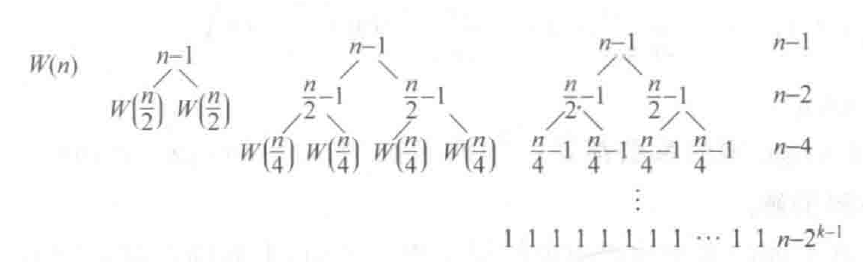
我们同样可以构造一个并不对称的递归树，如图2所示，这时我们讨论的就是所谓最坏情况的时间复杂度，由左边向下递归路径最短，而由右边向下递归的路径最长，这就对应着最坏情况的时间复杂度，我们应该计算右边节点的层数。

图2：非对称的递归树

直到第$k$层，我们应该有$\frac{2^k}{3^k}n=1$，此时$k=\log_{\frac32}n$，下面计算时间复杂度，我们需要将所有节点的权值加起来，每一层的节点相加都恰好为$n$，所以有：

$T(n)=n(k+1)=O(n\log n)$

尝试法

对于一些情况我们实在不会递推时，还可以使用尝试法进行一波猜测＋验证。例如在快速排序中：

$T(n)=\frac2n\sum_{i=1}^{n-1}T(i)+O(n)$

我们可以猜测：

$T(n)=C$，此时$LHS=O(1)$，而对于右边有 $RHS=\frac2n C(n-1)+O(n)=O(n)$，发现$LHS\neq RHS$，所以很遗憾，我们猜错了，重新猜。
$T(n)=cn$，这时$LHS=cn$，$RHS=\frac{2c}{n}\frac{n(n-1)}{2}+O(n)=cn-c+O(n)$，左边和右边一次项系数并不相同，所以很遗憾，又猜错了。
$T(n)=cn^2$，这时$LHS=cn^2$，$RHS=\frac2n\left[\frac{cn^3}{3}+O(n^2)\right]+O(n)=\frac{2c}{3}n^2+O(n)$，二次项系数还是对不上，所以这个解也不对。
$T(n)=cn\log n$，这时$LHS=cn\log n$，$RHS=\frac{2c}{n}\sum_{i=1}^{n-1}i\log i+O(n)$，对于这个求和，我们可以使用积分近似法来求出这个求和的上界。
$\sum_{i=1}^{n-1}i\log i\le\int_2^nx\log xdx=\frac{1}{\ln2}\left(\frac{n^2}{2}\ln n-\frac{n^2}{4}\right)-\frac{1}{\ln2}\left(2\ln2-1\right)$
这样不难看出这个求和的上界：
$\sum_{i=1}^{n-1}i\log i=\frac{n^2}{2}\log n-\frac{n^2}{4\ln2}+O(1)$
这样就对上了，所以这个时间复杂度是正确的，所以这个时间复杂度是对的，即$T(n)=O(n\log n)$。

另外，尝试法也可以计算一些带有取整函数的递推方程，例如如下的示例：

例题2 求解递推方程
$T(n)=2T\left(\lfloor\frac{n}{2}\rfloor\right)+n;~~~~T(1)=1$
对于没有取整时的递推方程的解为$O(n\log n)$，所以我们也估计原方程的解也是$cn\log n~~(n\ge2)$，我们可以进行归纳证明。

当$n=2$时，有$T(2)=2T(1)+2=4$，可以发现令$c=2$时有$T(2)\le c2\log2$。这时我们假设一切小于$n$的自然数$k$，都有$T(k)\le ck\log k$，那么我们就有：
$\begin{align} T(n)&=2T\left(\lfloor\frac{n}{2}\rfloor\right)+n\le2T(n/2)+n\le2c\frac n2\log\frac n2+n\\ &=cn(\log n-1)+n=cn\log n-cn+n\\ &\le cn\log n~~~~~~(c>1) \end{align}$
由数学归纳法，对于所有的$n$，都有$T(n)\le cn\log n$，所以$T(n)=O(n\log n)$。

【补充】这里我们用到了一些求和的函数，我觉得还是蛮有用的，所以在这里进行一个总结：
$\sum_{i=1}^{n-1}i\log i=\frac{n^2}{2}\log n-\frac{n^2}{4\ln2}+O(1)$ $\sum_{i=1}^{n}i^2=\frac16n(n+1)(2n+1)=O(n^3)$ $\sum_{i=1}^ni^3=\frac14n^2(n+1)^2$

主定理 (Master Theorem)

这部分是递推方程的核心内容，大部分递推方程都可以通过主定理来进行计算，所以遇到题目可以先尝试使用这个定理，如果不行再使用其他方法进行计算。下面我们先了解一下这个定理的内容：

定理6 设$a\ge1,b>1$为常数，$f(n)$为函数，$T(n)$为非负整数，且：
$T(n)=aT(n/b)+f(n)$
则有以下结果：

若$f(n)=O(n^{\log_ba-\epsilon})$，$\epsilon>0$，那么$T(n)=\Theta(n^{\log_ba})$。

若$f(n)=\Theta(n^{\log_ba})$，那么$T(n)=\Theta(n^{\log_ba}\log n)$。

若$f(n)=\Omega(n^{\log_ba+\epsilon})$，$\epsilon>0$，且对于某个常数$c<1$和所有充分大的$n$有$af(n/b)\le cf(n)$，那么$T(n)=\Theta(f(n))$。

注意这个$\epsilon$并不能通过$o$和$\omega$来替换$O$和$\Omega$消去，举个最简单的例子，$n$和$n\log n$这两个函数就完全不可能通过上面的三个情况来匹配，这也是一个不能应用主定理的例子。不妨通过例题来掌握这个方法的使用。

例题3 求解递推方程
$T(n)=9T(n/3)+n$
$a=9,b=3,f(n)=n$，那么$n^{\log_ba}=n^2$，有$f(n)=O(n^{2-\epsilon})$，这适用于主定理的第一条，我们可以选择$\epsilon=0.5$，我们可以得到$T(n)=\Theta(n^2)$。

例题4 求解递推方程
$T(n)=T(2n/3)+1\\ T(n)=3T(n/4)+n\log n$
分别适用主定理的第二条和第三条，答案分别为：
$T(n)=\Theta(\log n)\\ T(n)=\Theta(n\log n)$

我们说一个不能使用主定理的情况：

例题5 求解一下递推方程
$T(n)=2T(n/2)+n\log n$
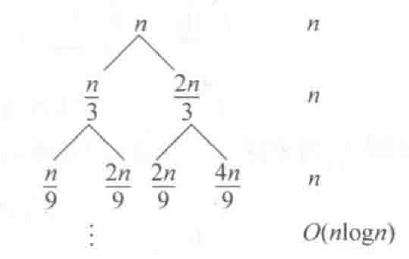
不难发现，这就是我们前面说的$n$和$n\log n$这两个函数完全无法与主定理的情况匹配的情况。这个递归方程我们不妨使用递归树进行计算：

图3：递归树的构建
如图三所示，我们可以构建这样的一个递归树来对应我们这个递推方程，我们可以求出这个树的层数$2^k=n$。整个问题的时间复杂度就是这个树的所有节点的和：
$T(n)=n\log n+n(\log n-1)+\cdots+n(\log n-2^k)=nk\log n+n(2^k-1)=n\log^2n+n^2-n$
所以递推方程的结果为：
$T(n)=O(n\log^2n)$

到此我们就已经学完了算法分析的全部内容。