实验-磁光Kerr效应
摘要: 平面偏振光在光洁磁极表面发生反射时,偏振面会出现微小偏转,这个现象被称为磁光克尔效应。磁光克尔效应反映了物质磁化状态对其光学性质的影响,属于磁光效应。克尔效应具有灵敏度高,转角精密的特点,所以近年来被用于超薄磁性膜[1],磁化动态过程[2]和自旋霍尔效应[3]的研究。本实验使用具有垂直磁各向异性的PtCo合金薄膜,利用光弹调制器使反射光强周期性变化,从而将微小的复克尔转角测量转化为光强测量。实验通过测量输出光强的直流、一次谐波和二次谐波信号,间接得到复克尔转角,并进一步利用复克尔转角测量PtCo合金薄膜的磁滞回线,进而得到样品的矫顽力和对应波长下的饱和克尔转角。实验对比不同起偏器角度下的克尔磁滞回线,分析起偏器角度误差对测量结果的影响。
关键词:磁光克尔效应(MOKE)、磁滞回线、光弹调制器
引言
理论基础
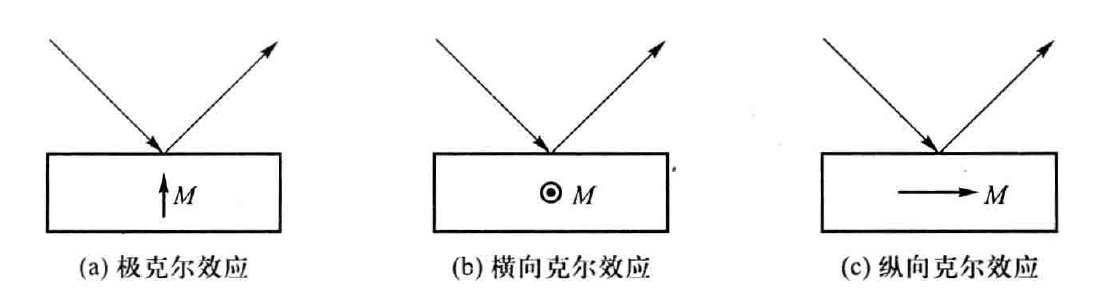
磁光克尔效应的分类
- 磁化方向垂直于介质反射面——极克尔效应
- 磁化方向平行于介质反射面但垂直于光入射面——横向克尔效应
- 磁化方向既平行于介质反射面又平行于光入射面——纵向克尔效应
克尔效应的唯象理论
其中,
其中,
称原x方向偏振分量
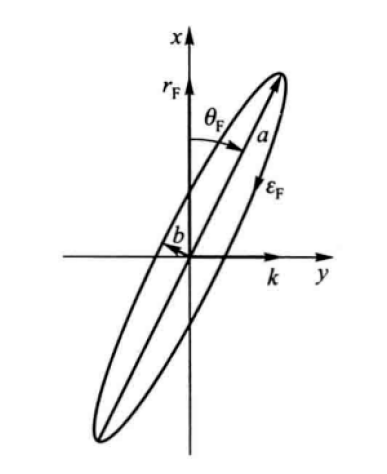
我们可以定义复克尔转角:
代入菲涅尔公式
其中,
磁光常量的动力学解释
设入射光为
其中,
实验仪器和材料介绍
样品
光弹调制器
锁相放大器
锁相放大器是一种交流电压表,能精确测定深埋在噪声之中周期重复信号的幅值及相位。具体电路包括:
- 相敏检波器
相敏检波器实际上是一个模拟乘法器,输出信号是输入信号 和参考信号 的乘积,包含差频和和频分量。 - 低通滤波器
器件内部噪声包括热噪声、散射噪声、闪烁噪声等。热噪声和散射噪声仅与测量频带宽度有关。可以通过压缩频带宽度减少。闪烁噪声可通过选取适当参考信号频率消除,低通滤波器输出特性为:
等效噪声带宽为:
低通滤波器时间常量
相关器
相敏检波器和低通滤波器统称为相关器。考虑输入信号是一埋没在噪声之中的微弱信号:
经过相敏检波器的过程可以被数学抽象为:
经过低通滤波器后就会除去大部分噪声:
同步积分器
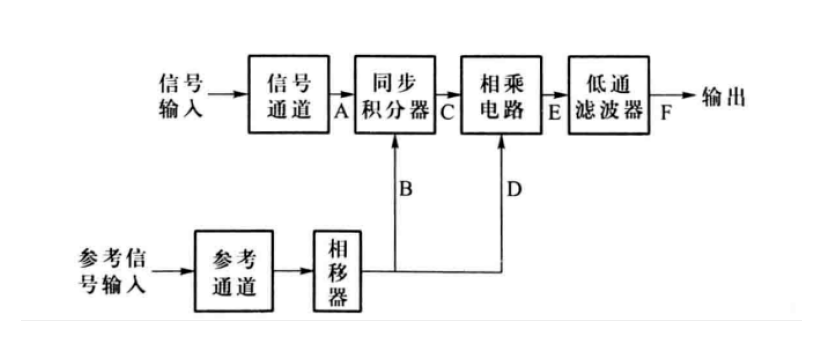
同步积分器是以参考信号频率为参量的方波匹配滤波器。与相关器区别在于同步器积分器输出一个与参考信号同频的方波信号,而相关器输出直流信号。锁相放大器原理图
如图3所示为单通道锁相放大器的原理示意图。其中,相移器的作用是改变已知参考信号的相位,通过相关器输出信号,确定待测信号振幅和相位。
Femto光电探测器和SCU-90信号整定器
Femto光电探测器是基于硅或铟镓砷(InGaAs)探测器,作用是将光信号转化为对应的电信号,便于观察和测量,探测频率范围
实验系统与测量原理
实验系统的组成
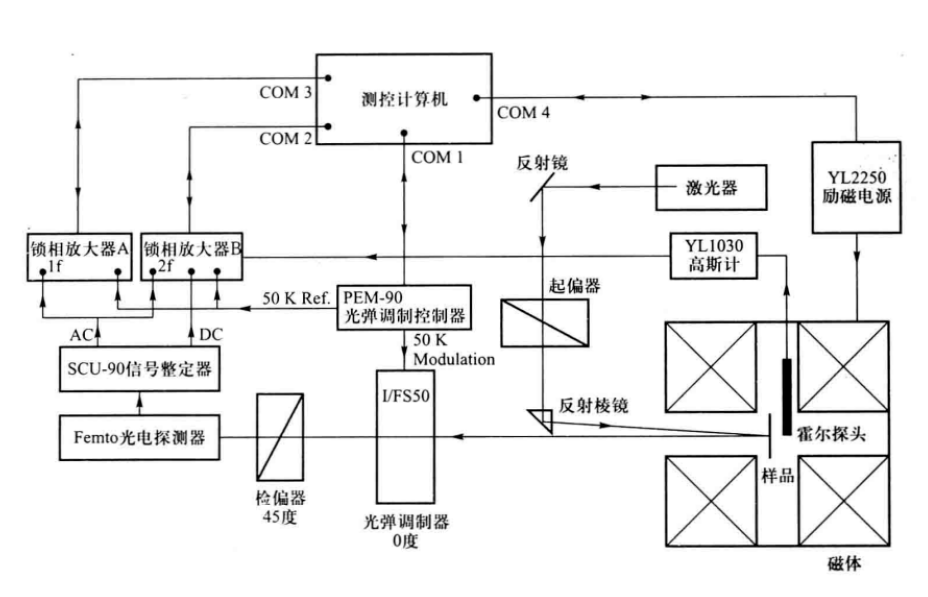
测量原理
其中,
其中,
光弹调制器产生的相位延迟是可以为人为控制的,我们定义其为:
如果取
根据这样的原理,我们可以通过两个锁相放大器读出发生克尔效应并经过光弹调制器和检偏器后的直流分量以及一次二次谐波振幅,进而得到克尔效应的转角和椭偏光的偏心率。我们在第二部分的理论分析中知道,克尔效应的转角和偏心率都是和金属的性质相关的,可以代表金属的磁化率,借此我们可以画出样品金属的磁化曲线。需要注意的是,由于整定器的放大作用,我们需要对输出的振幅进行重新的定标。
实验步骤
按以下步骤进行操作:
调节光路,使光学元件工作在最佳状态,并使光弹调制器的振动轴和起偏器偏振方向一致,使检偏器和起偏器偏振方向夹45°。
具体调节方法如下:调节样品架的每一个维度,使出射光直流分量光强,即锁相放大器B上显示的ADC1示数,达到最大值,此时光路达到最佳状态。然后调节检偏器,使直流分量光强最小,此时起偏器与检偏器正交;打开光弹调制器,旋转光弹调制器,使得直流分量光强最小,此时光弹调制器振动轴与起偏器通光方向一致;再将检偏器旋转45°,完成光路调节。
对测量系统定标,我们前面介绍仪器时讨论过Femto光电探测器和SCU-90信号整定器可能会使接受到的信号放大,从而需要对后续测量进行重新定标。
定标方法为:调节好起偏器、光弹调制器和检偏器的角度后,以30’为步长连续改变起偏器角度5次,每次测量克尔转角的相对值(实际上是仪器读出的二次谐波的振幅)。由于实验系统采用的是极克尔效应的模式,起偏器的角度并不影响金属膜的克尔效应,也就是说光经过金属膜就一定会被转角度,这样的条件下我们后续检测的公式就可以写成:
其中
利用计算机程序,测定金属膜的磁滞曲线。
具体做法如下:使用软件,在磁场为
到 范围内采集数据,得到克尔磁滞回线,从图中读出矫顽力和饱和克尔转角。最后将起偏器多次旋转几个角度,分别测量克尔磁滞回线,分析起偏器角度误差对磁滞回线零点位置的影响。
实验结果与分析讨论
测量系统的定标

金属膜的磁滞回线
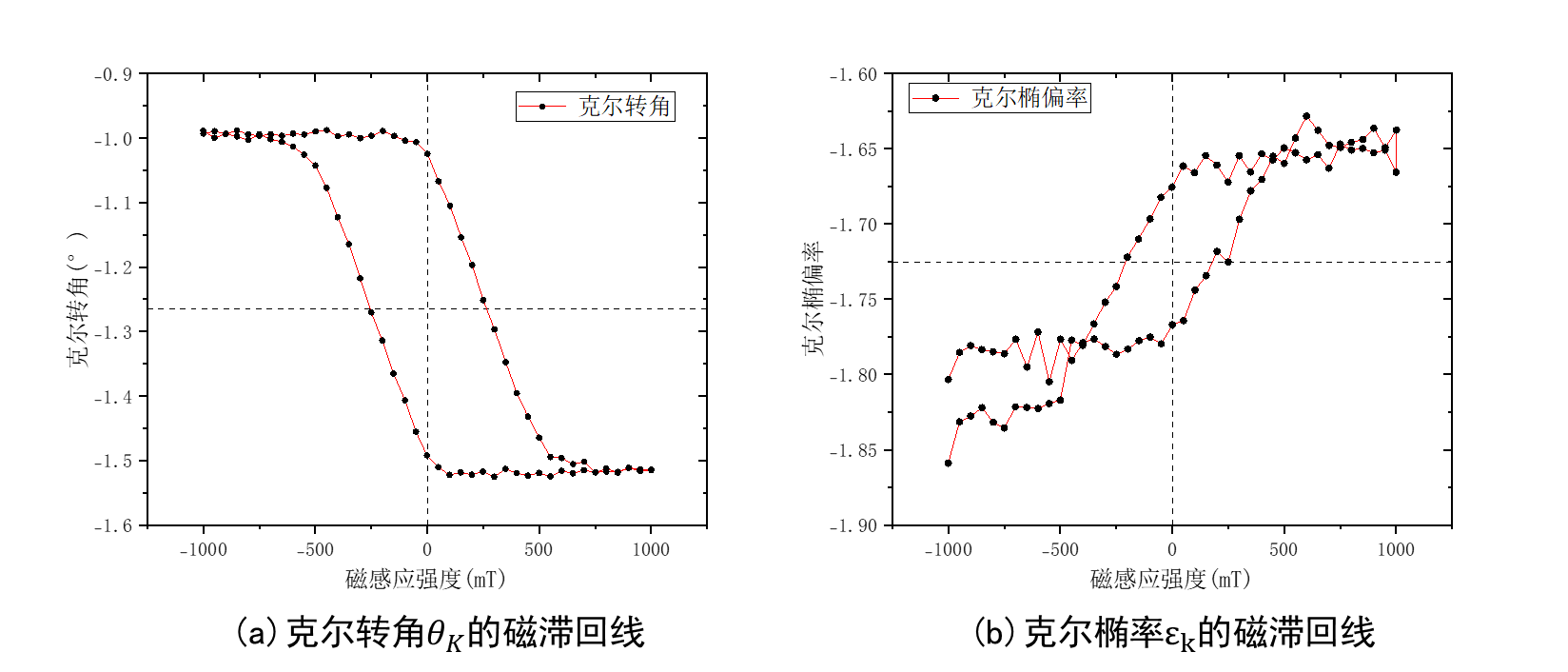
可以看到,克尔转角随着磁场变化,出现典型的磁滞现象,这表明样品PtCo合金具有铁磁性。同时,注意到克尔转角磁滞回线在
起偏器角度对克尔磁滞回线的影响
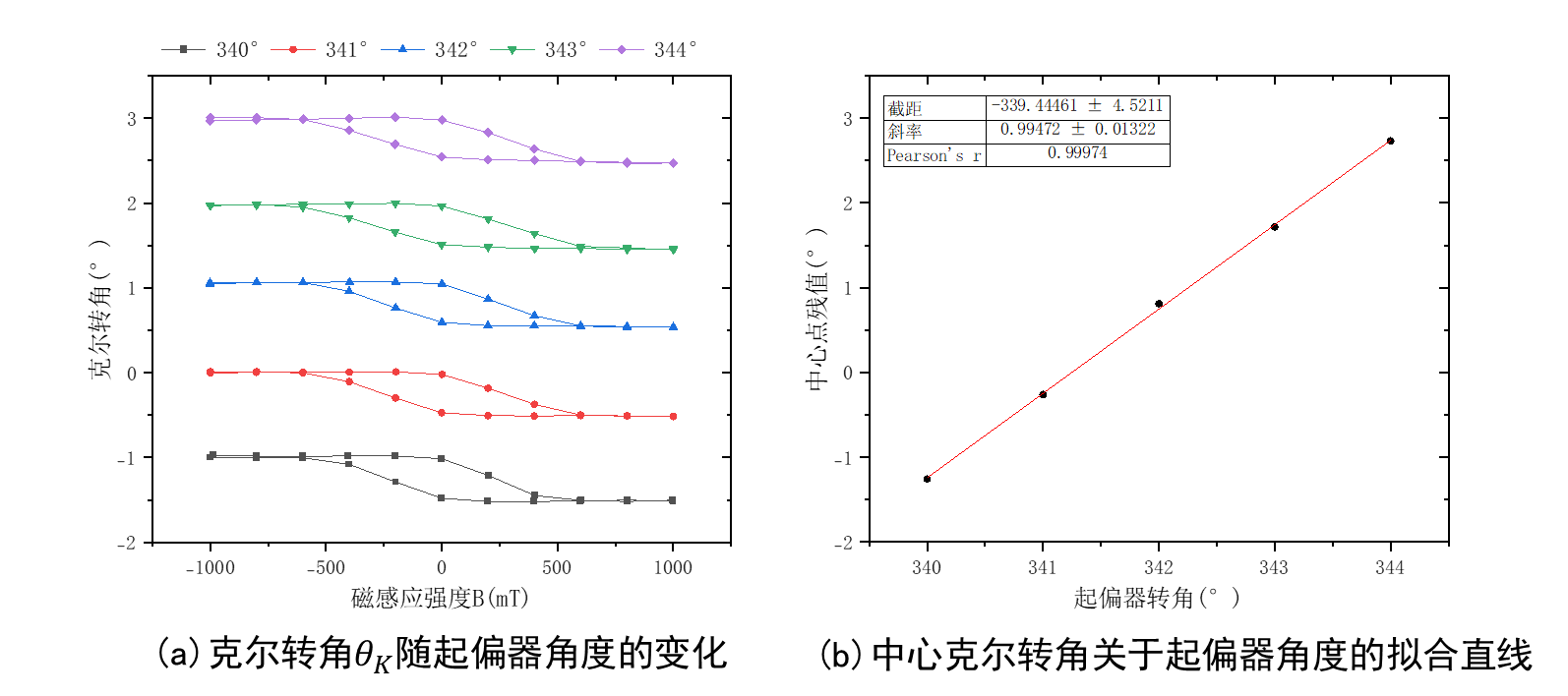
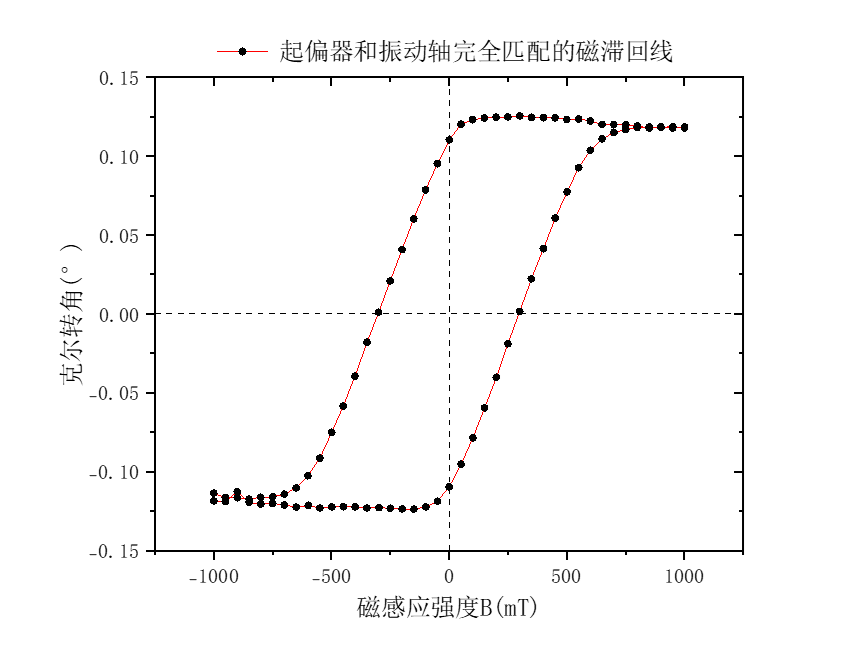
误差分析
偏振片和光弹调制器的偏转方向存在系统误差
一次谐波误差主要来自光弹调制器介质薄膜的多光束干涉
二次谐波的误差主要来自材料表面破损产生的二阶非线性效应
探究检偏器角度对于测量的影响
首先给出任意角度偏振片的琼斯矩阵:
假设起偏器的起振方向和光弹调制器的振动方向已经完全对齐,则对于实验的光学系统,可以通过下面的琼斯矩阵描述:
同样地代入
前三项为直流分量,第四项是一次谐波,和克尔椭偏率相关,最后一项是二次谐波,与克尔转角相关。同样选择
当检偏器被正确放置时,
根据上面三个方程联立,近似保留到
实验中更多依赖于克尔转角
对于每一个点的上下平移量为:
可以看出,每一个的平移量都各不相同,所以不同于起偏器的转角而言,检偏器的转角还会影响到磁滞回线的形状。我们通过图9来加强一下
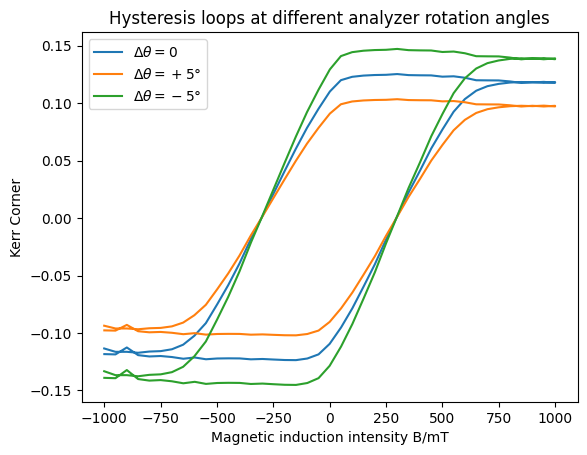
需要提前声明的是,图9默认了不同转角下测得的
结论
[1] ZHENG X Y, CHANNA S, RIDDIFORD L J, et al. Ultra-thin lithium aluminate spinel ferrite films with perpendicular magnetic anisotropy and low damping[J]. Nature Communications, 2023, 14(1): 4918.
[2] ALEBRAND S, BIERBRAUER U, HEHN M, et al. Subpicosecond magnetization dynamics in tbco alloys[J/OL]. Phys. Rev. B, 2014, 89: 144404. https://link.aps.org/doi/10.1103/PhysRevB.89.144404.
[3] SINOVA J, VALENZUELA S O, WUNDERLICH J, et al. Spin hall effects[J/OL]. Rev. Mod. Phys., 2015, 87: 1213-1260. https://link.aps.org/doi/10.1103/RevModPhys.87.1213.
[4] SUMI S, AWANO H, HAYASHI M. Interference induced enhancement of magneto-optical kerr effect in ultrathin magnetic films[J]. Sci. Rep., 2018, 8(1).
[5] WHITE A D, AHN G H, VAN GASSE K, et al. Integrated passive nonlinear optical isolators[J]. Nat. Photonics, 2023, 17(2): 143-149.
[6] HUANG H T, CHEN P J, GER T R, et al. Magneto-optical kerr effect enhanced by surface plasmon resonance and its application on biological detection[J/OL]. IEEE Transactions on Magnetics, 2014, 50(1): 1-4. DOI: 10.1109/TMAG.2013.2278189.
[7] HUANG D, LATTERY D, WANG X. Materials engineering enabled by time-resolved magneto-optical kerr effect for spintronic applications[J]. ACS Applied Electronic Materials, 2020, 3(1): 119-127.
[8] 荀坤吴思成. 近代物理实验(第四版)[M]. 高等教育出版社, 2015.
[9] 武燕婷李超波. 光弹调制器研究综述及原理验证[J/OL]. Review and Principle Verification of Photoelastic Modulator, 2019. DOI: 10.11977/j.issn.1004-2474.2021.03.013.
[10] CONTRIBUTORS W. Jones calculus — wikipedia, the free encyclopedia[EB/OL]. 2024. https://en.wikipedia.org/wiki/Jones_calculus.
[11] Wikipedia contributors. Fabry–pérot interferometer[EB/OL]. 2024. https://en.wikipedia.org/wiki/Fabry%E2%80%93P%C3%A9rot_interferometer.
Supplement:思考题
我们的实验装置对克尔转角和克尔椭偏率的测量精度是否一样高?为什么?
不一样高。克尔转角和克尔椭偏率分别于二次谐波和一次谐波分量幅度成正比,因此,二者的测量精度差异来源于系统对二次谐波和一次谐波分量幅度测量精度的不同。当光正入射到光弹调制器时,在其前后两个表面会发生多次反射,形成多光束干涉现象,导致一次谐波分量测量不准确,这可以从上述克尔椭率磁滞回线的畸变看出。因此,实验装置对克尔转角的测量精度要高于克尔椭偏率。
如果用一个以角速度
旋转的 玻片代替光弹调制器,光电探测器的输出信号会如何变化?能否测出复克尔转角? 给出旋转的
波片的琼斯矩阵为: 则可以给出出射光向量为:
则出射光强可以写成:
其中,
。从光强信号中我们仅能得到光强幅度,以及相位差两个量,无法从中得到克尔转角。

