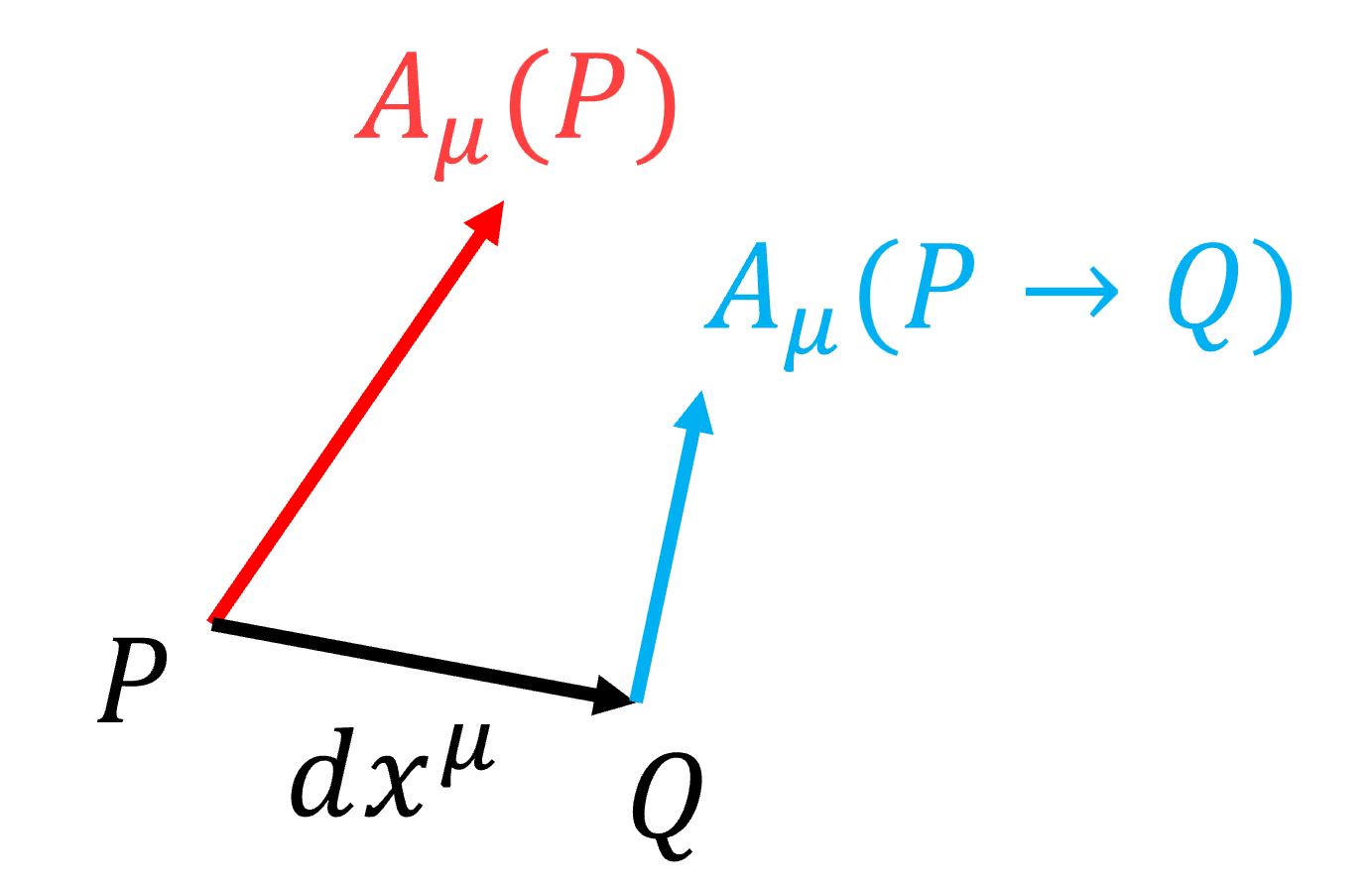张量及其运算

对于矢量的认知，可能在高中阶段的向量学习中就已经比较完善了，而对于矩阵以及他的运算，正常的同学一般会在刚上大学的线性代数课程中首次接触。在数学课程中，方阵一般代表一个线性方程组的系数矩阵，而对于学习物理学的同学而言，方阵的意义更多的是在n维空间内某一位置下一个当前空间的矢量的通量，例如动量密度矢量，它一般是一个的方阵，意味着空间中点处的动量大小和指向。

而张量这个概念则是更进一步的泛化“一组数”的概念。最开始接触张量的概念应该是在力学的学习中，刚体运动章节中一闪而过的转动惯量张量，或许当时就会有很多同学将张量和矩阵的概念画上等号了吧。然而，张量并非只能由行和列两个指标，它还可以是0个，1个，3个甚至无数个，按照我们的阶数观点来看的话，标量就是0阶张量，矢量就是1阶张量，而矩阵就是2阶张量。如果我们这样来看的话，张量的概念就又似乎被泛化为计算机中list的类型，似乎也不是物理上可以进行有物理意义运算的数学概念，我们还需要对这个量施以任何坐标中描述同一流形的要求，这样就得到了完整的所谓的张量。

以上谈的这些是我对张量这个概念的认知历程，之所以说这些，就是想告诉大家，张量这个数学概念是一个很有用的数学工具，对于研究物理的同学，争取使张量成为一个常用但不深究的概念便是极好的，如果你对下面的数学定义以及一些概念有更加深度的疑问，我也不会QWQ。

何为张量

在广义相对性原理中，我们认为物理规律与坐标系是无关的，坐标系只是人们认知世界的工具，而不能改变世界的客观事实。所以在广义相对论中，我们描述任何物理规律的方程都应该在任一坐标系中具有相同的形式，所以张量这个工具被拿了出来，我们之前规定了它在不同坐标系中可以描述同一个几何流形，所以将物理规律写成张量方程的形式就顺理成章了。

换成人话就是张量在两个坐标的变换中，其变换的规律和坐标变换的规律是相同的。例如，n维空间中的一个点为，而在另一个坐标系中，其坐标为，由此坐标变换可以写成：

$$\tilde{x}^\mu=\tilde{x}^\mu(x^1,x^2,\cdots,x^n)=\tilde{x}^\mu(x)$$

应用Einstein求和法则，坐标变换的微分形式为：

$$d\tilde{x}^\mu=\frac{\partial\tilde{x}^\mu}{\partial x^\alpha}dx^\alpha$$

不难看出，是一个矩阵（或者叫二阶张量更符合我们今天的主题ovo），如果它的行列式不为0，则坐标变换存在逆变换：

$$dx^\alpha=\frac{\partial x^\alpha}{\partial\tilde{x}^\mu}d\tilde{x}^\mu$$

这时我们再来看张量的变换，首先，对于零阶张量（标量），他没有任何指标，所以定义其变换应满足：

$$\tilde{T}(\tilde{x})=T(x)$$

对于一阶张量（矢量），存在一个指标，定义其满足如下变换：

$$\tilde{T}^\mu=\frac{\partial\tilde{x}^\mu}{\partial x^\alpha}T^\alpha$$

而对于二阶张量，存在两个指标，我们定义其变换为：

$$\tilde{T}^{\mu\nu}=\frac{\partial\tilde{x}^\mu}{\partial x^\alpha}\frac{\partial\tilde{x}^\nu}{\partial x^\beta}T^{\alpha\beta}$$

可以看出，在坐标变换中，张量的每一个指标都按坐标微分的变换进行变换，这一点对于更高阶的张量也是成立的。

张量的指标不一定全在上面，我们称写在张量右上角的指标为上指标或逆变指标，在右下角的为下指标或者协变指标，注意逆变指标的变换规则同坐标的微分变换一致，而协变指标的变换规则则是和坐标微分的逆变换一致。对于只有上指标的张量，称为逆变张量，而对于只有下指标的张量，称为协变张量，当然，也有上下指标均有的张量，我们就称其为混合张量。

eg1：给出混合张量的坐标变换：

注意两种指标分别满足不同的变换规则

$$\tilde{T}^\mu_\nu=\frac{\partial\tilde{x}^\mu}{\partial x^\alpha}\frac{\partial x^\beta}{\partial\tilde{x}^\nu}T^\alpha_\beta$$

张量的运算

基本运算

1. 加减法和数乘：

   $$C^\mu_{\nu\alpha}=kA^\mu_{\nu\alpha}-B^\mu_{\nu\alpha}$$

2. 外积：

   $$C^\mu_{\nu\alpha}=A^\mu_\alpha B_\nu$$

3. 缩并（内积）：

   $$C_\nu=C^\mu_{\nu\mu}$$

当然，我们还可以定义一些便于我们后面运算的操作，例如对称张量（），记为：

$$T^{(\mu\nu)}=\frac{1}{2}(T^{\mu\nu}+T^{\nu\mu})$$

另外还有反对称张量（），记为：

$$T^{[\mu\nu]}=\frac{1}{2}(T^{\mu\nu}-T^{\nu\mu})$$

最后需要注意的是，对于张量，我们要时刻注意保持其性质，即流行不依赖于坐标，所以以上所有操作均需要在空间内同一个点进行，在不同点上的减法运算很容易减出一个不是张量的数组，这是不符合物理意义和张量定义的减法。例如求导这个操作在大部分时候都是不满足张量性质的：

$$\frac{\partial W_{\nu'}}{\partial x^{\mu'}}=\frac{\partial x^\mu}{\partial x^{\mu'}}\frac{\partial}{\partial x^\mu}\left(\frac{\partial x^\nu}{\partial x^{\nu'}}W_\nu\right)$$

我们将分量表达式按正常偏导进行计算可得：（注意这里的和是两套坐标）

$$\frac{\partial W_{\nu'}}{\partial x^{\mu'}}=\frac{\partial x^\mu}{\partial x^{\mu'}}\frac{\partial x^\nu}{\partial x^{\nu'}}\frac{\partial W_\nu}{\partial x^\mu}+W_\nu\frac{\partial x^\mu}{\partial x^{\mu'}}\frac{\partial}{\partial x^\mu}\frac{\partial x^\nu}{\partial x^{\nu'}}$$

可以看出对于一个张量的正常坐标变换，多出了后面的第二项，如果那么这个求导运算仍然是合法的，但是一般情况下，这一项都不是0，求导运算在张量中不成立，这是我们求导学家不能接受的，下面我们就探讨一下如何通过更好的方式来定义张量的求导。

更严格的求导——张量的平移

我们可以想想一个并不平直的空间（也许你可以想象球面），上面的一个张量（你可以想象一个矢量），我们想求这个张量的导数，并且要求这个导数值仍然是一个张量，那么我们不妨将张量沿着非平直空间进行平移，将两个张量平移到一起去，在同一个位置进行加减运算，这样我们就满足了上述条件，但不难想到，平移的过程中，张量必然会发生变化。我们现在就来评估这种变化。

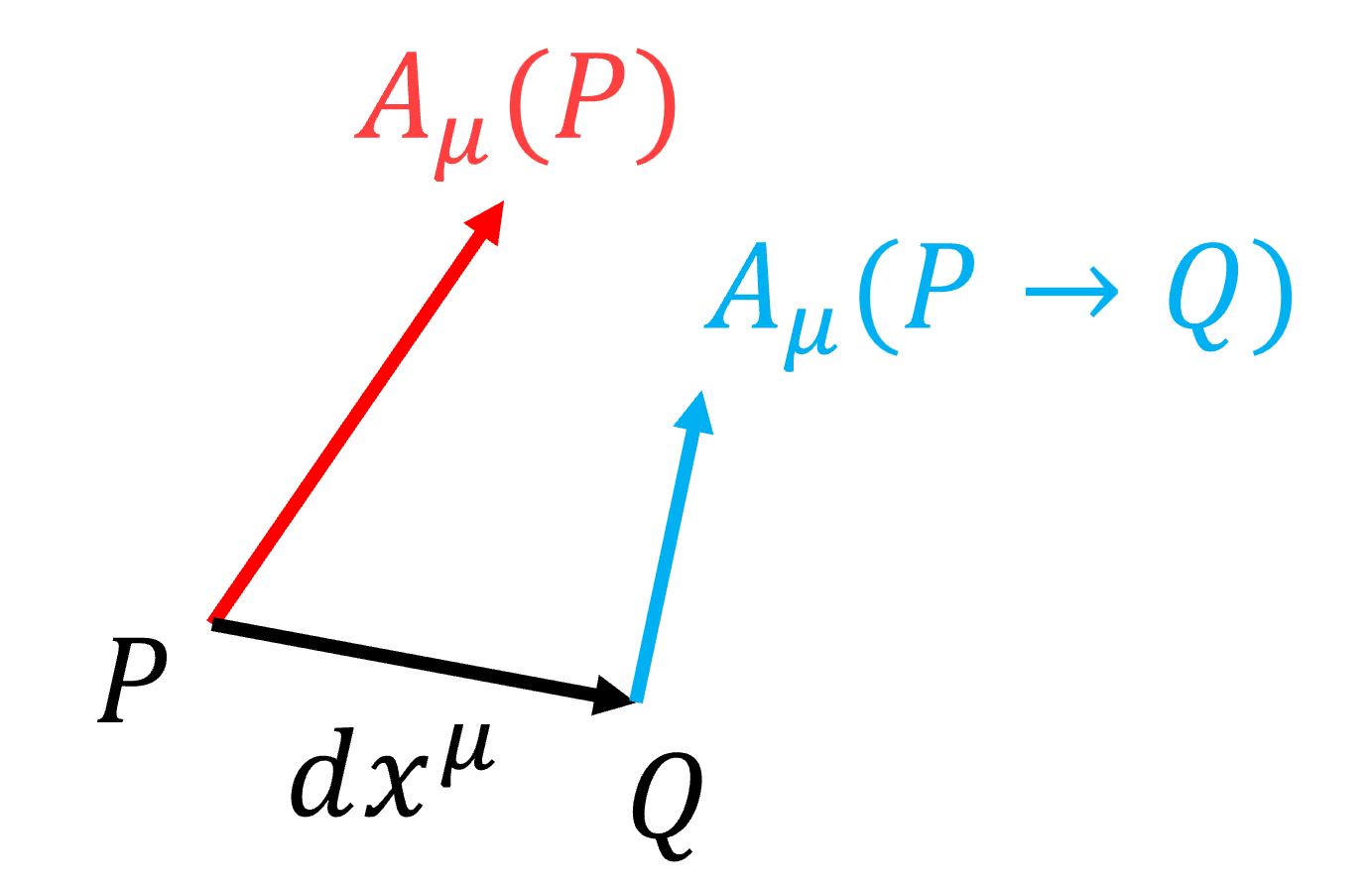
图1：张量平移示意图

如图1所示，我们将P点的张量平移到Q点，得到的张量为。既然是张量，首先应该满足张量的坐标变换的规则：

$$\tilde{A}_\mu(P\to Q)=\left(\frac{\partial x^\alpha}{\partial\tilde{x}^\mu}\right)_QA_\alpha(P\to Q)$$

其中，中间的坐标部分可以通过泰勒展开将P点和Q点的导数产生关联

$$\left(\frac{\partial x^\alpha}{\partial\tilde{x}^\mu}\right)_Q=\left(\frac{\partial x^\alpha}{\partial\tilde{x}^\mu}\right)_P+\left(\frac{\partial^2x^\alpha}{\partial\tilde{x}^\mu\partial\tilde{x}^\nu}\frac{\partial\tilde{x}^\nu}{\partial x^\sigma}\right)_Pdx^{\sigma}$$

另一方面，我们先假设张量平移满足仿射联络变换：

$$A_\mu(P\to Q)-A_\mu(P)=\Gamma^\lambda_{\mu\nu}(P)A_\lambda(P)dx^\nu$$

其中，称为仿射联络，之所以不叫它仿射联络张量是因为这个玩意不是张量，后面我们会证明。我们在P点可以将同样按方程(17)写成：（以下物理量如果不标括号就是P点的）

$$\tilde{A}_\mu+\tilde{\Gamma}^\lambda_{\mu\nu}\tilde{A}_\lambda d\tilde{x}^\nu=\tilde{A}_\mu(P\to Q)=\left(\frac{\partial x^\alpha}{\partial\tilde{x}^\mu}+\frac{\partial^2 x^\alpha}{\partial\tilde{x}^\mu\partial\tilde{x}^\nu}\frac{\partial\tilde{x}^\nu}{\partial x^\sigma}dx^\sigma\right)A_\alpha(P\to Q)$$

我们再将代入并展开，扔掉二阶项，我们有：

$$\tilde{\Gamma}^\lambda_{\mu\nu}\frac{\partial x^\beta}{\partial\tilde{x}^\lambda}\frac{\partial\tilde{x}^\nu}{\partial x^\sigma}=\frac{\partial^2 x^\beta}{\partial\tilde{x}^\mu\partial\tilde{x}^\rho}\frac{\partial\tilde{x}^\rho}{\partial x^\sigma}+\Gamma^\beta_{\alpha\sigma}\frac{\partial x^\alpha}{\partial\tilde{x}^\mu}$$

将坐标的矩阵通过逆矩阵乘到右侧，得：

$$\tilde{\Gamma}^\tau_{\mu\gamma}=\frac{\partial^2 x^\beta}{\partial\tilde{x}^\mu\partial\tilde{x}^\gamma}\frac{\partial\tilde{x}^\tau}{\partial x^\beta}+\Gamma^\beta_{\alpha\sigma}\frac{\partial x^\alpha}{\partial\tilde{x}^\mu}\frac{\partial\tilde{x}^\tau}{\partial x^\beta}\frac{\partial x^\sigma}{\partial\tilde{x}^\gamma}$$

观察方程(20)可以看出，除非右侧第一项为0，否则几何联络都不是张量，仿射联络的选取也并不是唯一的，对于广义相对论的话，我们会更喜欢使用对称的联络：

$$\Gamma^\lambda_{(\mu\nu)}=\frac{1}{2}(\Gamma^\lambda_{\mu\nu}+\Gamma^\lambda_{\nu\mu})$$

对于非对称部分称为挠率张量(torsion)，至少在较浅的广义相对论中没有这个东西啥事。

张量的协变微商

利用前面定义的仿射联络，我们可以将一个张量平移，进而使定义一个最符合物理意义的微商成为可能，我们称这个操作为协变微商。我们可以给出其定义（以一阶张量为例）

$$T_{\mu;\nu}\equiv\lim_{Q\to P}\frac{T_\mu(Q)-T_\mu(P\to Q)}{\Delta x^\nu}$$

注意后面的普通微商我们用’,’来表示(如果不知道普通微商定义的话可以参考方程(23))，协变微商我们用’;’来表示。接下来我们从不同阶数的张量入手，来介绍以下协变张量和普通张量的关系。

标量

对于标量，由于它没有指标，坐标变换中根本不发生变化，所以其普通微商和协变微商是相同的。

$$T_{,\mu}\equiv\frac{\partial T}{\partial x^\mu}=T_{;\mu}$$

矢量

对于一个协变矢量，我们可以通过方程(22)来求得协变矢量的协变微商，我们可以得到关系：

$$T_{\mu;\nu}=T_{\mu,\nu}-\Gamma^\lambda_{\mu\nu}T_\lambda$$

当然对于协变微商，我们仍然要求莱布尼兹法则对协变微商成立，这样我们就可以利用标量的协变微商和普通微商相同来确定逆变矢量的两种微商的关系：

$$A^\mu_{;\lambda}B_\mu+A^\mu B_{\mu;\lambda}=(A^\mu B_\mu)_{;\lambda}=(A^\mu B_\mu)_{,\lambda}=A^\mu_{,\lambda}B_\mu+A^\mu B_{\mu,\lambda}$$

将方程(24)代入方程(25)中，可以得到：

$$T^\mu_{;\lambda}=T^\mu_{,\lambda}+\Gamma^\mu_{\sigma\lambda}T^\sigma$$

更高阶张量(以二阶张量为例)

我们只需要对所有指标都进行仿射变换就好，我们以二阶张量为例，给出它的变换规则：

$$T_{\mu\nu;\lambda}=T_{\mu\nu,\lambda}-\Gamma^\rho_{\mu\lambda}T_{\rho\nu}-\Gamma^\rho_{\nu\lambda}T_{\mu\rho}$$ $$T^{\mu\nu}_{;\lambda}=T^{\mu\nu}_{,\lambda}+\Gamma^\mu_{\rho\lambda}T^{\rho\nu}+\Gamma^\nu_{\rho\lambda}T^{\mu\rho}$$ $$T^\mu_{\nu;\lambda}=T^\mu_{\nu,\lambda}+\Gamma^\mu_{\rho\lambda}T^\rho_\nu-\Gamma^\rho_{\nu\lambda}T^\mu_\rho$$

测地线方程

在欧式几何中，我们对直线情有独钟，在完全空间中也是相同的，我们称之为测地线，对于曲线上的切矢量：

$$A^\mu(P)=\left(\frac{dx^\mu}{d\lambda}\right)_P$$

如果满足，则称为测地线。仔细想想这个定义是合理的，就是说一条线上所有的协变微商平行，在平直空间中也是十分合理的。

由矢量的平移：

$$A^\mu(P\to Q)=\frac{dx^\mu}{d\lambda}-\Gamma^\mu_{\alpha\beta}\frac{dx^\alpha}{d\lambda}\frac{dx^\beta}{d\lambda}d\lambda$$

另一方面，我们通过泰勒展开，有：

$$A^\mu(Q)=A^\mu(P)+dA^\mu(P)=\frac{dx^\mu}{d\lambda}+\frac{d^2x^\mu}{d\lambda^2}d\lambda$$

二者有平行关系：

$$A^\mu(Q)=(1+f(\lambda))A^\mu(P\to Q)$$

当我们保留到的一阶项，得到测地线方程为：

$$\frac{d^2x^\mu}{d\lambda^2}+\Gamma^\mu_{\alpha\beta}\frac{dx^\alpha}{d\lambda}\frac{dx^\beta}{d\lambda}=f(\lambda)\frac{dx^\mu}{d\lambda}$$

其实，我们还可以选取更好的参量来使方程(34)化简。假设：

$$\lambda=\lambda(\sigma)$$

那么我们有：

$$\frac{dx^\mu}{d\lambda}=\frac{dx^\mu}{d\sigma}\frac{d\sigma}{d\lambda}$$ $$\frac{d^2x^\mu}{d\lambda^2}=\frac{d^2x^\mu}{d\sigma^2}\left(\frac{d\sigma}{d\lambda}\right)^2+\frac{dx^\mu}{d\sigma}\frac{d^2\sigma}{d\lambda^2}$$

代入式(34)中我们可以得到：

$$\left(\frac{d^2x^\mu}{d\sigma^2}+\Gamma^\mu_{\alpha\beta}\frac{dx^\alpha}{d\sigma}\frac{dx^\beta}{d\sigma}\right)\left(\frac{d\sigma}{d\lambda}\right)^2=\frac{dx^\mu}{d\sigma}\left(f(\lambda)\frac{d\sigma}{d\lambda}-\frac{d^2\sigma}{d\lambda^2}\right)$$

这时，如果满足：

$$\frac{d^2\sigma}{d\lambda^2}=f(\lambda)\frac{d\sigma}{d\lambda}$$

这样我们可以得到最简的测地线方程：

$$\frac{d^2x^\mu}{d\sigma^2}+\Gamma^\mu_{\alpha\beta}\frac{dx^\alpha}{d\sigma}\frac{dx^\beta}{d\sigma}=0$$

这个测地线方程也可以由哈密顿原理得到，可以给出作用量为：

$$\tau=\int^{P_2}_{P_1}\sqrt{-g_{\mu\nu}\frac{dx^\mu}{d\lambda}\frac{dx^\nu}{d\lambda}}d\lambda$$

到此为止吧，如果想知道怎么推导的话可以康康刘川老师的《理论力学》。

曲率张量

经过上面的讨论，我们似乎已经可以构建一个广义相对论的图景，然而我们还有一个最大的问题，几何联络并非一个张量，而我们曾经说过，对于广义相对性原理，我们的物理规律应由张量方程构成，也就是说我们搞半天定义的联络根本不能单独出现在方程中。也就是说我们现在必须好好想想如何构造几个张量用于描述时空的几何性质。

最简单的一个就是我们前面偷偷提到的挠率，但是可惜在对称联络中，挠率为0，所以我们还得另作他算。我们想到了曲率这个量。考察：

$$\begin{align} A_{\lambda;\mu;\nu}&=A_{\lambda;\mu,\nu}-\Gamma^\rho_{\lambda\nu}A_{\rho;\mu}-\Gamma^\rho_{\mu\nu}A_{\lambda;\rho}\\ &=A_{\lambda,\mu,\nu}-\Gamma^\rho_{\lambda\mu,\nu}A_\rho-\Gamma^\rho_{\lambda\mu}A_{\rho,\nu}-\Gamma^\rho_{\lambda\nu}A_{\rho,\mu}+\Gamma^\rho_{\lambda\nu}\Gamma^\sigma_{\rho\mu}A_\sigma-\Gamma^\rho_{\mu\nu}A_{\lambda,\rho} \end{align}$$

取对和的反对称组合，我们可以整理并定义：

$$A_{\lambda;[\mu;\nu]}\equiv\frac{1}{2}(A_{\lambda;\mu;\nu}-A_{\lambda;\nu;\mu})=\frac{1}{2}(R^\rho_{\lambda\mu\nu}A_\rho-2\Gamma^{\rho}_{[\mu\nu]}A_{\lambda;\rho})$$

因此，我们不做解释的定义出了曲率张量，也称为黎曼张量：

$$R^\rho_{\lambda\mu\nu}=\Gamma^\rho_{\lambda\nu,\mu}-\Gamma^\rho_{\lambda\mu,\nu}+\Gamma^\sigma_{\lambda\nu}\Gamma^\rho_{\sigma\mu}-\Gamma^\sigma_{\lambda\mu}\Gamma^\rho_{\sigma\nu}$$

我们不妨给出曲率张量的一些性质：

1. 曲率张量有两个指标是反对称的：

   $$R^\rho_{\lambda\mu\nu}=-R^\rho_{\lambda\nu\mu}$$

2. 当时，则空间时平坦的。